Научный журнал

Международный журнал экспериментального образования

ISSN 2618–7159

ИФ РИНЦ = 0,425

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Дроздов А.М. 1 Жохов А.Л. 2

---

1 Криворожский педагогический университет

2 Ярославский педагогический университет

Важнейшая космологическая проблема современности – определение состояния Вселенной в любой наперед заданный момент времени, включая наполняющие её материальные части. Решение проблемы возможно можно лишь для ее циклической модели, в которой энтропия цикла равна нулю, а механизм эволюции работает абсолютно точно, подчиняясь принципам детерминизма Канта-Лапласа. Границы цикла с предельно высокой вероятностью могут быть установлены границами количественной области применения ОТО. Поскольку эта область проявляет себя за огромный отрезок времени, то определить ее опытным путем невозможно. В статье предложен опосредствованный путь на основе определения пределов структурных превращений динамического варианта геометрии Минковского, группа преобразований которой выступает инвариантной группе преобразований ОТО. Взятая за основу вместо геометрии Римана, она позволила осуществить решение космологической проблемы в шести приближениях с определением важнейших количественных показателей эволюции Вселенной.

Статья в формате PDF

0 KB

космологическая проблема

область применения общей теории относительности

n-мерный вариант геометрии Минковского

циклическая модель эволюции Вселенной

интервал переменных значений скорости света

эволюция периодической системы химических элементов

метапериод

«стрелы времени» цикла Вселенной

Абсолютный мир

физическая природа феноменов жизни и разума

1. Азимов А. Я робот. – К.: Веселка. – 1987. – 271 с.

2. Амосов Н.Н. Алгоритмы разума. – К.: Наукова думка. – 1965. – 164 с.

3. Дроздов А.М., Макареня А.А., Старова Т.В. Новый подход в исследовании верхней границы Периодической системы // Химия в школе. – 2012. – №9. – С.5-9.

4. Дроздов А.М., Дроздов Е.А., Стригунов В.И. Моделирование интеллекта и подсознание // Философские исследования. – 1993. – №1. – С. 161-169.

5. Дроздов А.М., Жохов А.Л., Дроздов Е.А. Возможная модель Вселенной (геометрия Минковского и ее приложение) // Труды ХI международных Колмогоровских чтений. ЯГПУ, МГУ. – 2011. – С.107-112.

6. Дроздов А.М., Жохов А.Л. Модель эволюции Вселенной на основе варианта геометрии Минковского //European social science journal. – М.: МИИ, 3 (42), том 1, 2014.– С.8-17.

7. Дроздов А.М., Макареня А.А., Жохов А.Л. Периодическая система как завершенное целое с прогнозированием физических свойств элементов 7-11 периодов // Химия в школе. – 2014. – №8. – С.4.

8. Бор Н. Избранные научные труды, т.1. – М.: Наука, 1970. – С. 291.

9. Жохов А.Л. Становление и развитие мировоззрения индивида образованием и культурой. Монография – Heinrich-Böcking-Str. Saarbrücken, Germany: Palmarium Academic Publishing. – 2014. – 404 с.

10. Бронштейн И.Н., Семендяев Е.А. Справочник по математике. – М.: Наука. – 1965. – С.70.

11. Dirak P.A. Proc. Soc. A. 117. 610 (1928) 118. 356.

12. Зоммерфельд А. Строение атома и спектры. – М.: Изд. техн. литер. – 1956. С.134.

13. Кедров Б.М. Теоретические основы материалистической диалектики // Вопросы философии. – 1976. – №12. – С. 52-66.

14. Комова Е.Г. Группа химических астероидов. – М.: Просвещение, 1964. – С.172.

15. Менский М.В. Квантовые измерения, феномен жизни и стрела времени: связь между тремя великими проблемами // Успехи физических наук, т. 177. – №4. – 1995. – С. 422.

16. Минковский Г. Пространство и время. – М.: Атомиздат. – 1973. – С.173.

17. Перельман В.И. Краткий справочник химика. Изд. третье. – 1954. – С.15.

18. Rydberg I The originals of the elements and the high frequency spectra // Phil. Mag. – 1914. Vol. 28 – Р. 144-149.

19. Эйнштейн А. Собрание научных трудов в 4-х томах. Т.1. 1965. – С. 201, 219, 320, 383, 392.

20. Эйнштейн А. О «космологической проблеме»: Собрание научных трудов в 4-х томах. Т. 2, 1966. – С.612.

Работа по созданию эволюционирующей циклической модели Вселенной была начата авторами в 80-х годах ХХ столетия [Дроздов А.М., Жохов А.Л., Дроздов Е.А. 1988: 1-10]. Дальнейшее ее развитие вылилось в формулировку новой теории относительности в качестве высшей ветви релятивизма – теории Абсолютного мира [Дроздов А.М., Жохов А.Л., Дроздов Е.А. 2011: 107-112]. Вторично работа была апробирована в 2014 году в докладе на международной научной конференции «Гуманитарные науки и современность» (Москва, 30 марта 2014). Работа была опубликована в материалах конференции [Дроздов А.М., Жохов А.Л. 2014: 8-17]. Тогда же был выдан авторам «Акт о внедрении результатов исследования и их апробации» научно-внедренческим центром Международного исследовательского института.

На этом этапе работа носила теоретический характер, создающий основу для прикладных исследований. Данная статья, посвященная решению космологической проблемы, является началом таких прикладных исследований в области мегамира на основе авторских модели и теории Абсолютного мира. Таким образом, новый этап авторских исследований мегамира и его результаты вызвали необходимость в написании этой статьи.

… в первом приближении

Космологическая проблема, сформулированная в 20 столетии, гласит: определить состояние Вселенной в любой наперед заданный момент времени [Эйнштейн А. 1966: 612]. Такое определение накладывает ограничение на выбор модели эволюции Вселенной: решение космологической проблемы возможно лишь для модели циклической Вселенной, в которой частота колебаний и длина волны неизменны для всех мыслимых циклов.

Чем же определяются пределы, в каких совершается колебательное движение циклической Вселенной? Очевидно, они определяются областью применения ОТО. Однако А. Эйнштейн определил эту область качественно, как всеобщую, подобно всеобщим законам сохранения энергии, массы и т.д., что явно недостаточно для решения космологической проблемы. Количественная же область применения ОТО до сих пор не известна. Таким образом, начало в решении космологической проблемы должно быть заключено в количественном определении области применения ОТО.

Поскольку область применения ОТО есть одновременно также и область движения Вселенной внутри ее двух пределов, то ее вначале надо определить не только пространственно (расстоянием), но и временно (длительностью) с помощью фундаментального параметра. Таким фундаментальным параметром является скорость света, которую для классической теории относительности принято считать бесконечно большой в сравнении со скоростью любых тел, а для специальной теории относительности – конечной и постоянной в отсутствии или при постоянстве гравитации. В СТО скорость света является верхним пределом движения тел. А так как ОТО включает в себя в качестве частных случаев классическую и специальную теории относительности, то и для ОТО показателем области применения должна быть скорость света. Однако она должна быть специфической именно для ОТО. Эту специфику определил для ОТО Альберт Эйнштейн в качестве переменной величины в условиях переменного гравитационного поля [Эйнштейн А. 1965: 210, 219, 320, 385, 392].

Отсюда ясно, что показателем области применения ОТО является не сама по себе переменная скорость света, а ее интервал, реализующийся в фазе расширения (сжатия) за невообразимо большой промежуток времени. Это исключает всякую возможность его опытного определения. Эйнштейн не предпринял попытку определения этого интервала, вероятно, понимая невозможность опытного его измерения и не видя для этого иной возможности.

В данной работе сделана попытка исследования возможного определения интервала переменных значений скорости света на основе изменения структуры динамического варианта геометрии Минковского. Сам Минковский подал пример динамического подхода к исследованию, доказывая инвариантность групп преобразований СТО и классической механики допущением: «Пусть «с» стремится к бесконечности». Тогда 1/с стремится к нулю (рис. 1) , и геометрия Минковского превращается в геометрию Галилея [Минковский Г. 1973: 173].

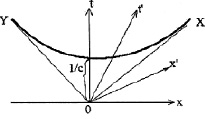
Рис. 1. Четырехмерная геометрия Минковского

Идя вслед за Минковским, можно определить наряду с установленным им одним пределом другой предел путем исследования максимального превращения структуры динамической геометрии допущением: «Пусть «с» стремится к нулю». Тогда 1/с стремится к бесконечности, угол «светового конуса» АОВ (рис. 2) стремится к 180 градусам, а фигура, подобная двуполостному гиперболоиду вращения, вырождается в две параллельные плоскости.

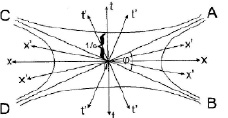
Рис. 2. Плоскостное сечение симметричного варианта геометрии Минковского (АОВ – угол «светового конуса»)

Таким образом, динамический вариант геометрии Минковского обладает двумя пределами превращений: при «с = ∞» ее метрика вырождается в метрику линии – одномерного пространства, при «с = 0» ее метрика вырождается в метрику цилиндрического пространства. Сам же интервал переменных значений скорости света оказывается показателем количественной области применения ОТО. Динамический вариант геометрии Минковского не отбрасывает геометрию Римана, а, с позиции принципа соответствия, превращает последнюю и в частные случаи геометрии Галилея, вступая в роль основной и ведущей геометрии естествознания.

Однако в ОТО, построенной для условия переменного гравитационного поля, не может быть использован 4-мерный вариант геометрии Минковского, разработанный для обоснования специальной теории относительности (СТО). Ведь последняя справедлива для условия отсутствия или постоянства гравитации. Для ОТО необходим такой вариант геометрии Минковского, который в ее структуре отводит место тяготеющим массам. В этом отношении симметрия исходных фигур этой геометрии, подобных одно и двуполостному гиперболоидам вращения, а также метрика пространственно-подобных квадрантов позволяют определить в структуре геометрии Минковского область двух симметричных тяготеющих масс в форме двояковыпуклых линз. При этом возникает необходимость в бесконечном количестве сопряженных между собой систем отсчета, поскольку геометрическое описание движения тел сводит тело любого размера к точке, а геометрическое рассмотрение движения объемного тела приводит к необходимости рассмотрения одновременного движения бесконечного количества точек. Бесконечное количество сопряженных систем отсчета для симметричной геометрии Минковского можно получить процедурой бесконечного плоскостного сечения, проходящего через ось симметрии Вселенной. В результате получаем n-мерный вариант геометрии Минковского, являющийся одновременно и моделью моментального снимка одного из бесчисленных этапов эволюции Вселенной.

Такая геометрия представлена на рис. 3. Она обладает наряду с основными элементами симметрии симметрией вещества и спинового вращения тел из-за неголономности пространства. К такой модели применимы закон симметрии вещества Дирака Е = 2mc2+T [Dirac Р. 1928: 118] и фейнмановская теория античастиц, согласно которой тела, описываемые моделью, можно назвать миром и антимиром.

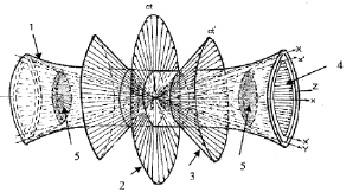
Рис. 3. N-мерный вариант геометрии Минковского: 1 – фигура, подобная однополостному гиперболоиду вращения; 2 – плоскость осей координат времени покоящихся систем отсчета; 3 – поверхность конуса координат времени движущихся систем отсчета; 4 – конус координат пути движущихся систем отсчета; 5 – область системы двух тел, отвечающих закону симметрии вещества Дирака

Закон Дирака, имея в качестве слагаемых компонент гравитационную и кинетическую энергии, дает основу для построения механики изолированной системы в виде цикла, состоящего из двух фаз – расширения и сжатия – двух сингулярных состояний материи, с одной стороны, чисто электромагнитного, а с другой – чисто вещественного (нейтронного). В фазе расширения угол светового конуса АОВ (рис. 2) изменяется от 0 до 180 градусов. Форма силового взаимодействия двух миров (гравитационная волна) определится их поверхностью и даст вместе с конфигурацией тел единую сферу Вселенной, претерпевающей эволюцию (рис. 4) от вытянутого эллипсоида вращения через шар к сплюснутому эллипсоиду вращения. Последняя форма вырождается в цилиндр. На шарообразной стадии наблюдается выравнивание продольной и поперечной деформации тел, что приводит к временной изотропии пространства.

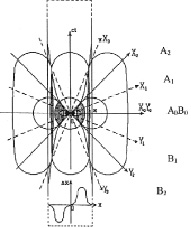
Рис. 4. Геометрия движения Абсолютного мира. В нижний части рисунка график колебательного движения, описывающий фазу расширения вселенной

В фазе сжатия с изменением угла «светового конуса» от 180 до 360 градусов те же конфигурации Вселенной изменяются в обратном направлении. Факторами движения тел Вселенной в фазе расширения являются кинетическая энергия и энтропия, а в фазе сжатия – соответственно гравитация и нэгэнтропия.

С точки зрения изложенной концепции отпадает необходимость исследования знака кривизны пространства на данной стадии эволюции Вселенной, выдвинутая Эйнштейном [Эйнштейн А. 1966: 612]. Положительная кривизна присуща сфере двух тел, отрицательная кривизна – псевдосфере, описываемой процессом эволюции каждого из миров. Псевдосфера и есть тот частный случай, который в общей геометрии Минковского представлен геометрией Римана. Общая схема движения Вселенной на каждом цикле одинакова, но наполнение их индивидуальными системами различно. Поэтому каждый цикл представляет собой Универсум, а бесконечное их число, какое можно назвать термином Абсолютный мир, предложенным Минковским, состоит из неограниченного множества Универсумов.

Всё, кратко изложенное выше, дает возможность сформулировать периодический закон эволюции Вселенной: переменные конфигурации тел мира и антимира, а также конфигурации образуемой ими гравитационной волны находятся в периодической зависимости от ускорения их относительного движения; ускорение этих тел есть функция переменной скорости света, связанной с углом «светового конуса» геометрии Минковского.

Тем самым получено решение космологической проблемы в первом приближении.

Приложение к первому разделу

Решение космологической проблемы оказалось возможным на основе выдвижения новой теории относительности в качестве высшей ветви релятивизма – теории Абсолютного мира [Дроздов А.М., Жохов А.М., Дроздов Е.А. 2011: 107-115] [Дроздов А.М., Жохов А.Л. 2014: 8-17]. Как и известные теории относительности, теория Абсолютного мира обладает собственной геометрией, спецификой скорости света и количественной области применения, а также инвариантностью группы пространственно-временных преобразований с аналогичными группами преобразований трех известных теорий относительности. В частности, инвариантность групп Абсолютного мира и ОТО проявляется в том, что n-мерный вариант геометрии Минковского при наложении на него интервала переменных значений скорости света описывает псевдосферу – пространство геометрии Римана ОТО, деформированное тяготеющей массой тела. Кроме того, формулировкой периодического закона эволюции Вселенной установлена геометрическая форма инвариантности объема различных стадий циклического движения. Для завершения теории Абсолютного мира необходимо найти аналитическое выражение этого инварианта.

Что же принципиально нового утверждает эта теория? Она утверждает циклический характер движения тел на самом высоком уровне организации материи. Периодический процесс движения тел описывается двумя терминами: «пульс» и «цикл». Из этих двух терминов в современной космологии предпочтение отдано первому, лежащему в основе так называемой «пульсирующей» модели Вселенной. Какова же причина того, что циклическая модель не вызывает интереса космологов в качестве насущной и актуальной проблемы? Цикл движения заключен между двумя четкими пределами, в отличие от этого пульсация характеризуется колебаниями внутри неких потенциально возможных, но никогда не досягаемых пределов. Выбор пульсирующей модели объясняется тем, что космологии не просто неизвестны пределы колебательного движения Вселенной, но сообщество ученых сегодня отказывается признавать правомерным такую постановку космологической проблемы. Ведь даже начало расширения Вселенной в виде так называемого «ноль-пункта времени» не является пределом, хотя ему и придан масштаб порядка 10-33 сантиметра, что на 24 порядка меньше атома химического элемента. С точки зрения этой научной сказки-фантазии, все вещество Вселенной сжато здесь до ничтожного размера частицы, какая все же имеет объем, отличный от нуля, чтобы спасти природу от абсурда бесконечной плотности вещества. Непредвзятый взгляд на это состояние Вселенной даёт понять, что здесь зафиксировано предельное состояние не только пространства и времени, но и материи. Во Вселенной два действующих объекта: вещество и электромагнитное поле. Если на пределе сжатия отсутствует вещество вследствие аннигиляции и Вселенная находится в электромагнитном состоянии, то плотность вещества становится равной нулю. При этом пространственная составляющая Вселенной в ее энергетическом эквиваленте становится эквивалентной одномерному пространству.

Что касается второго предела рассматриваемого цикла, то он представляет собой нейтронное состояние вещества в отсутствии электромагнитного поля с расположением частиц в двух плоскостях – основаниях цилиндра – с толщиной плоскости, равной диаметру нейтрона. Таким в виде одной структурной единицы вещества представляется состояние максимальной энтропии циклической Вселенной, поскольку продукт естественного «старения» и атома, и анти-атома является нейтроном. Следовательно, каждое из двух сингулярных состояний материи во Вселенной выступает результатом определенной аннигиляции: «начало» расширения – результатом аннигиляции вещества вместе с его симметрией, «конец» расширения – результатом аннигиляции только симметрии вещества. При этом симметрия вещества жестко не определяет материю каждого из тел Вселенной одним из миров: тело, бывшее «миром» в фазе расширения, становится «антимиром» в фазе сжатия с соответствующим набором частиц антивещества.

Циклическая модель позволяет дать объяснение отсутствию в наблюдаемой части Вселенной антивещества пространственным разделением вещества и антивещества в самое первое мгновение рождения вещества из электромагнитного поля.

Предлагаемая нами модель Вселенной требует, конечно, опытного обоснования существования антимира. Но очевидно, что данных прямого наблюдения антимира сейчас нет так же, как 100 лет тому назад не было получено опытных фактов, указывающих прямо на планетарную модель атома. Резерфорд воспользовался уже известными данными об электрической природе атома и добавил к ним те, которые были получены в самостоятельном эксперименте. Планетарная модель явилась результатом обобщения всех этих косвенных данных. Такие же непрямые, косвенные данные современной космологии известны. Поскольку их не может объяснить традиционная (стандартная) модель Вселенной, они названы «темной энергией» и «темной материей». Развиваемая нами симметричная модель Вселенной объясняет эти эффекты дальнодействием гравитационной и кинетической энергии невидимого антимира на наш мир.

Наконец, специфика количественной области применения теории Абсолютного мира, в отличие от ОТО, заключается в удвоенном интервале значений переменных скорости света, которые реализуются в обеих фазах жизни Вселенной количественно одинаково, но лишь в противоположной направленности (от бесконечности до нуля в фазе расширения и от нуля до бесконечности в фазе сжатия). При этом физический смысл бесконечной скорости света в отсутствии вещества приобретает значение неопределенно большой величины, а нулевая скорость – значение, которое можно принять для «чисто» вещественной стадии Вселенной.

Полученная модель Абсолютного мира, построенная на динамическом варианте геометрии Минковского и на представлении Эйнштейна о переменной скорости света, является идеальной моделью. Ее развитие во втором, третьем и т.д. приближениях с учетом дополнительных факторов превращает ее в реальную модель, вступающую на путь совершенствования, которому нет конца.

… во втором приближении

Конкретизация полученного в первом разделе варианта решения космологической проблемы может быть осуществлена путем установления количественной связи между скоростью света и величиной угла «светового конуса» геометрии Минковского, а также между возрастом каждого из этапов эволюции Вселенной и углом «светового конуса».

Для этого воспользуемся законом Хаббла, утверждающим, что Вселенная в настоящее время находится в изотропном состоянии, так как скорость расширения ее одинакова во всех направлениях, что согласуется с наблюдениями. В изотропном состоянии угол «светового конуса» полученной нами модели Вселенной равен 90 градусам. А поскольку в геометрии Минковского скорость света находится в линейной зависимости от угла «светового конуса», то появляется возможность установления графической зависимости между этими величинами. Однако скорость света согласно СТО не зависит от направления движения источника света, то есть не является величиной векторной. А потому она не различается знаками плюс и минус в фазах расширения и сжатия. Как же при этом можно отразить противоположно направленный процесс реализации интервала переменных значений с в фазах расширения и сжатия Вселенной?

Разрешить это противоречие можно путем установления связи переменной скорости света и скорости относительного движения двух тел Вселенной. Эти величины практически равны, когда скорости этих тел на каждом этапе меньше скорости света лишь на бесконечно малую величину, чтобы кинетическая энергия движения Вселенной на каждом его этапе отвечала условию, необходимому для выполнения максимальной работы. На этом основании можно построить график зависимости скорости относительного движения тел мира и антимира. Он представлен на рис. 5, а полученные на его основе данные сведены в табл. 1. Абсолютные значения этих величин являются переменными величинами скорости света. Построен этот график на двух точках с координатами «90 градусов (–300000 км/с)» и «270 градусов (+ 300000 км/с)».

Для расчета времени прохождения всех этапов эволюции Вселенной воспользуемся подобной же линейной зависимостью времени от угла «светового конуса» в геометрии Минковского. В графических координатах «время – угол «светового конуса»» наносим точку, отвечающую значению аргумента 90 градусов, и функции – в 15 миллиардов лет – современному возрасту Вселенной, считая при этом «стрелу времени» необратимой. Соединим эту точку прямой линией с началом отсчета системы координат и продлим ее до той точки, которая соответствует аргументу в 180 градусов. Этому этапу фазы расширения Вселенной отвечает бесконечное время. Бесконечное время в отсутствии электромагнитного поля принимает значение неопределенно большой величины. На графике (рис. 5) такая величина изображена вертикальной пунктирной прямой линией. Из полученного графика можно найти промежуток времени любого этапа эволюции Вселенной.

Время этапов фазы сжатия Вселенной определяем по принципу обратимости времени в сравнении с фазой расширения, когда угол «светового конуса» геометрии Минковского изменяется от 180 до 360 градусов (рис. 6) табл. 2.

Таблица 1

Скорости относительного движения тел Вселенной в соответствии с этапами их движения

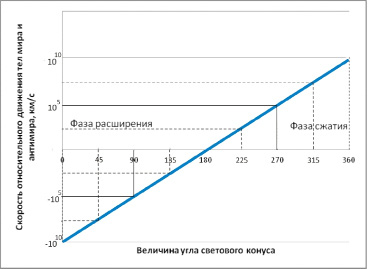
Рис. 5. График изменения скоростей относительного движения тел за цикл Вселенной

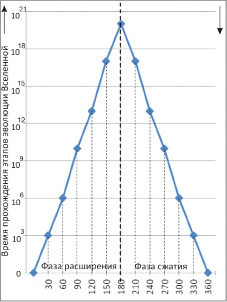
Рис. 6. График возраста этапов эволюции Вселенной

Таблица 2

Время каждого их этапов эволюции Вселенной, отвечающих величине угла «светового конуса»

Тем самым получено решение космологической проблемы во втором приближении с установлением основных показателей процесса эволюции Вселенной: переменной скорости света, скорости движения тел мира и антимира и времени каждого из бесконечного количества этапов эволюции Вселенной.

… в третьем приближении

Только сингулярные состояния материи (электромагнитное и нейтронное) и области, расположенные вблизи них, не представляют атомного состояния материи. Все остальные этапы эволюции Вселенной представлены атомным строением вещества. Оно определяет следующий по значимости аспект космологической проблемы, касающийся эволюции химических элементов, поскольку этот процесс составляет органическое единство с процессом эволюции Вселенной.

В настоящее время среди ученых наметилась тенденция считать периодический закон и периодическую систему химических элементов Д.И. Менделеева обоснованными только квантово-механической теорией строения атома. Она объяснила причину периодичности в строении атомов элементов и нашла корреляцию места элемента, группы и периода в квантовых числах. Но эта теория не нашла такой корреляции для самой большой структурной единицы периодической системы – диады, установленной Ридбергом в начале 20 столетия [Rydberg 1914: 145]. Вероятно, такое обоснование диады надо ожидать со стороны эволюционной теории периодической системы, еще не созданной, но интуитивно сформулированной в конце Х1Х века как учения о неорганическом дарвинизме [Кедров 1976: 52-56].

Во второй половине ХХ столетия остро встал вопрос о верхней границе периодической системы, и он несомненно является также вопросом эволюции химических элементов. Метод «атом-аналогии» Менделеева не дает возможности прогнозировать ее верхнюю границу. Прогноз осуществляют на основе явления радиоактивности и гипотетической оболочечной модели ядра атома, а также вытекающих из нее «магических чисел» нуклонов. Размывание периодичности в области тяжелых атомов, якобы, свидетельствует об исчерпании полного объема системы в районе второй сотни химических элементов.

Квантово-механическая теория, по свидетельству Н. Бора [Бор1970:291] и А. Зоммерфельда [Зоммерфельд 1956: 134], строилась на данных химической систематики и спектроскопическом материале. Из них статистической обработке надо было подвергнуть лишь данные спектроскопии, так как химическая систематика в виде периодической системы уже содержала в себе результаты предшествующей статистики (период, группу и место элемента). В квантовой модели атома они нашли точное преломление в квантовых числах.

Очевидно, новая теория периодической системы должна строиться при наличии другой фундаментальной проблемы и ещё не описанных атомной теорией структурных единиц системы. И то, и другое периодическая система имеет в качестве эволюционной проблемы и самой большой структурной единицы, не получившей объяснения.

Если с рядом периодов: 1 2 3 4 5 6 7 связывают электронное

2 8 8 18 18 32 32

заполнение атомных оболочек, то с рядом диад:

1 11 111 1У

4 16 36 64

не связывают никакую квантово-механическую информацию.

Очевидно, вместе с рядом элементов ряд периодов и ряд диад составляют три уровня организации периодичности химических элементов:

1. зависимость свойств элементов от порядкового номера (Z);

2. зависимость мощности периодов от порядкового номера периода (n);

3. зависимость мощности диад от порядкового номера диады (Q).

Это дает возможность использовать метод статистической обработки данных периодической системы применительно к трем уровням организации периодичности.

Следует отметить, что рассмотрение периодичности до сих пор ограничивалось лишь первым уровнем, для которого, в отличие от двух других, известно множество рядов (рис. 7). Такое различное представительство этих уровней требует положить в основу метода исследования второго и третьего уровней организации периодичности получение для них такого же множества, как и для первого уровня [Дроздов, 2012: 5].

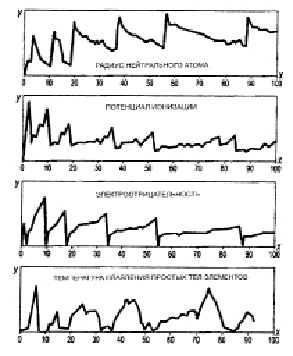
Рис. 7. Ряды элементов

Суммированием значений величин определенного параметра химических элементов в пределах периодов получаем ряд чисел, характеризующих мощности периодов – ряд периодов. Множество рядов периодов будет обусловлено множеством использованных параметров элементов. Графики этих рядов свидетельствуют о том, что во многих случаях наблюдается отсутствие монотонности роста мощности периода с возрастанием его номера (рис. 8). Основываясь на этом и пользуясь элементами математического метода параболической интерполяции [Бронштейн 1965: 70], для получения рядов диад используем не только сложение полученных мощностей, но и вычитание величин меньшего из большего по номерам периодов внутри диады. Графики рядов диад представлены на рис. 9, 10.

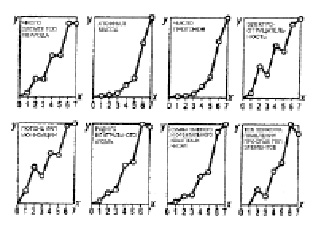
Рис. 8. Ряды периодов

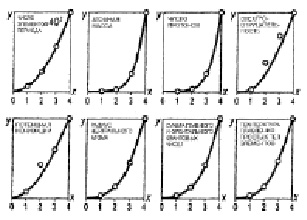
Рис. 9. Ряды диад, полученные суммированием мощности периодов

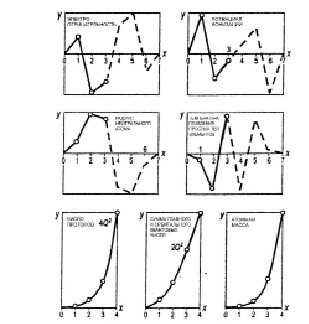
Рис. 10. Ряды диад, полученные разностью мощности периодов

Статистическое сопоставление графиков рядов всех трех уровней организации периодичности свидетельствует о том, что последовательный переход от первого уровня к третьему имеет тенденцию к математическому упрощению. Если графики первого уровня имеют большое число изломов, а графики второго уровня – меньшее число изломов, то графики третьего уровня в целом выражаются параболической закономерностью. Лишь несколько рядов диад выпадают из общей картины, что можно объяснить либо исключением из общего правила, либо подчинением другой функциональной зависимости, представленной на рис. 10 возвратно-поступательной волной.

Предпочтительность второго допущения можно обосновать следующим образом. Если первый уровень организации периодичности дал возможность выделить период, а второй уровень – более крупную структуру – диаду, то третий уровень, будучи равноправным с первыми двумя, должен нести информацию о новой более крупной структурной единице периодической системы.

Благодаря своим периодическим свойствам новая структурная единица системы может быть названа мета-периодом. Оценка мощности мета-периода, рассчитанная по формуле для одного периода диады N = 2Q2, дает значение 362 элемента. Из них 86 приходится на первую полуволну, относящуюся к фазе расширения Вселенной, остальные – на вторую полуволну, относящуюся к фазе сжатия. Такое разделение ряда химических элементов по частям мета-периода совпадает с границей стабильности элементов. Действительно, стабильны элементы от начала периодической системы вплоть до конца шестого периода, что, по выражению Г. Сиборга, не оставляет надежд на возможность существования «островков стабильности в море нестабильности».

С изложенной точки зрения, диада – определенный этап (одна седьмая часть) в реализации мета-периода. Из них шести основным периодам цикла одного из миров Вселенной отвечает шесть диад мета-периода, представленных атомным строением вещества. Сам же мета-период выступает как самая крупная структура периодической системы в силу отсутствия информации о химических элементах второго, третьего и так далее циклах Вселенной.

Очевидно, эволюция периодической системы химических элементов выступает в качестве частного случая эволюции Вселенной, что позволяет следующим образом сформулировать закон эволюции периодической системы: число диад мета-периода однозначно определяется числом периодов цикла эволюции одного из миров Вселенной.

Современные представления о верхней границе периодической системы крайне противоречивы. Согласно одной точке зрения, основанной на строении ядра, объем системы ограничен рамками второй сотни. Противоположная ей точка зрения (высказанная Гольданским), вытекающая из постулата квантовой механики о значении главного квантового числа, допускает потенциальную бесконечность системы, буквально в несколько миллиардов элементов [Комова 1964: 172]. Развиваемые нами взгляды о колебательном характере эволюции периодической системы позволяют найти диалектическое разрешение этих противоречий: бесконечный ряд элементов в эволюционном плане реализуется через конечную серию, описываемую мета-периодом.

Тем самым получено решение космологической проблемы в третьем приближении.

…в четвертом приближении

Рассчитанному количеству (362) химических элементов завершенной периодической системы весьма строго отвечает ее длинно-периодическая форма, включающая в себя s-, p-, d-, f-, g-, h- элементы. Такая форма системы представлена на рис. 11. Выполненные исследования [Дроздов 2014: 4] показали, что авторская форма системы дает возможность осуществления прогноза физических свойств элементов на фазе сжатия Вселенной.

На первых порах можно ограничиться прогнозом физических свойств основных четырех групп элементов: щелочных, щелочноземельных металлов, галогенов и инертных газов.

При этом воспользуемся методом, основанным на известной логарифмической форме зависимости физической величины от другой величины. В качестве этой другой величины, выступающей в данном случае в роли аргумента естественно выбрать логарифм главного квантового числа или номер периода системы. Получаемые при этом графические линейные зависимости можно экстраполировать на область 7-11 периодов фазы сжатия Вселенной.

Построенные графические зависимости характеризуются высокими коэффициентами аппроксимация. Они позволяют осуществить прогноз атомных масс, радиусов атомов и потенциалов ионизации для указанных четырех групп элементов в фазе сжатия Вселенной. Однако в целях экономии места в статье в качестве примера приведем лишь один график (рис. 12). Ему отвечает коэффициент аппроксимации, равный 0,994.

Количественные результаты осуществленного прогноза сведены в табл. 3-4. Необходимые для этого исходные величины взяты из справочных данных [Перельман 1954:15] [Романова: 2004: 408].

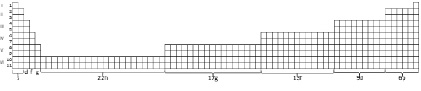
Рис. 11. Завершенная периодическая система в объеме 362 элементов

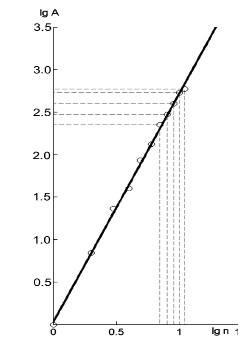
Рис. 12 Логарифмический график зависимости атомной массы щелочных металлов от порядкового номера периода или главного квантового числа

Таблица 3

Относительные атомные массы элементов с 1 по 11 период

Таблица 4

Прогноз радиусов нейтральных атомов и потенциала ионизации элементов

Величины полученных физических свойств свидетельствуют о нарастании металлических и ослаблении металлоидных свойств, что может говорить о высокой реакционной способности элементов в фазе сжатия Вселенной.

…в пятом приближении

Среди многочисленных космологических идей ХХ столетия высказывалась и такая, согласно которой в модели циклической Вселенной реализуется только одна «стрела времени» – энтропийная. В такой модели Вселенной цикличность носит искусственный характер, поскольку движению Вселенной положен лишь один предел – «ноль-пункт времени», в то время как циклическое движение возможно только внутри двух пределов. И каждый из них должен представлять собой особое качественное состояние материи. В отсутствии второго предела расширению движение вспять не может быть оправдано наличием одних сил тяготения. На пределе расширения система должна войти в состояние максимальной энтропии, выше которой энтропия уже не может быть фактором самопроизвольного течения процесса. В фазе сжатия самопроизвольное движение должно определяться не только фактором энергетическим (гравитацией), но и фактором упорядоченности – стремлением системы к максимальной негэнтропии. Гравитация как слабая сила не может сама по себе обеспечить обратимость времени.

Стремление к максимальной негэнтропии и вызовет к жизни новую уже негэнтропийную «стрелу времени». Если в фазе расширения фактор гравитации (притяжение) противостоял действию факторов ускорения (кинетической энергии и энтропии), то в фазе сжатия факторами ускоренного движения выступают и гравитация, и негэнтропия.

С представлением о «стреле времени» тесно связаны представления о физике и феномене жизни. Первое понятие («стрела времени») объединяет два других (физику и феномен жизни). При этом если в циклической Вселенной реализуется только одна «стрела времени», то это означает, что в природе имеет место только одна направленность событий, только одна физика. Такая версия утверждает абсолютную монополию второго закона термодинамики в природных процессах и делает невозможным разработку естественно-научного представления о сущности жизни. Живые организмы, не только не основанные на росте энтропии, но ведущие с ней в онтогенезе и филогенезе непримиримую борьбу, перед лицом единственной физики, провозгласившей монополию на процесс возрастания энтропии, выступают явлением чудесным, случайным и отнюдь не космическим.

Однако в современной термодинамике нет такой монополии на процесс возрастания энтропии. Второе начало термодинамики допускает наряду с доминирующей направленностью событий также и противоположную направленность, вероятность которой ничтожно мала. Это означает, что феномен жизни имеет под собой пусть и ничтожно малое, но вполне естественнонаучное основание. А чтобы феномен жизни приобрел по-настоящему космическое звучание, необходимо второе начало термодинамики признать симметричным в объеме вселенского цикла. При этом в фазе расширения доминирующим надо будет признать энтропийную направленность физических событий, энтропийную «стрелу времени» и энтропийную физику, а в фазе сжатия – негэнтропийную «стрелу времени» и такую же физику.

С позиций симметрии 2-го закона термодинамики феномен жизни – это достаточно яркое проявление в среде доминирующего физического процесса ему противоположного, который является доминирующим уже в другой фазе циклической Вселенной. Иными словами, жизнь в расширяющейся Вселенной отражает направленность событий физики сжимающейся Вселенной, а жизнь в сжимающейся Вселенной отражает направленность событий физики энтропийной фазы Вселенной.

Таким образом, решение космологической проблемы в пятом приближении позволяет сделать вывод о существовании во Вселенной двух физик и двух биологий. Бытующее же мнение о том, что термодинамика не может быть использована для объяснения как Вселенной, так и феномена жизни, поскольку не предназначена для описания единственного объекта, несостоятельно. Ведь при бесконечном количестве циклов в Абсолютном мире бесконечно много как Вселенных, так и феноменов жизни, хотя в полуцикле Вселенной – жизнь это космический феномен в единственном числе в каждом из миров.

… в шестом приближении

Наряду с феноменом жизни выступает еще один важнейший космологический феномен – р а з у м . На первый взгляд кажется, что разум – всего лишь предикат феномена жизни, и космическим он является только в рамках живого. Однако почти столетнее развитие кибернетики показало, что разум в отличие от феномена жизни может быть смоделирован в лаборатории на неживой матрице. Эта обретаемая независимость разума от феномена жизни подчеркивает статус космологической самостоятельности разума во Вселенной.

Однако оппоненты могут возразить, что кибернетике пока удалось смоделировать лишь элементы разума, а не сам разум в целом, хотя большинство специалистов-кибернетиков вообще отрицает существование какой-либо аналогии между человеческим и искусственным интеллектом. Из тех ученых, которые верят в возможность машинного разума, можно сослаться на Н.Н. Амосова [Амосов Н.Н. 1905: 304], который считает, что машина будет обладать искусственным разумом лишь тогда, когда в ее программу будут записаны все интеллектуальные свойства человека.

Вопреки такому утверждению авторы данной статьи считают, что для искусственного разума нужно ввести в компьютер дополнительную программу, моделирующую всего одно важное человеческое качество, чтобы машина уже сегодня приобрела способность рассуждать и мыслить [Дроздов А.М., Дроздов Е.А., Стригунов В.И. 1993: 161-167]. В авторской модели человеческий интеллект представлен двумя уровнями: сознанием и подсознанием. Сознание напрямую связано с волеизъявлением индивидуума, и потому присуще всем высшим животным. Оно отключается в состоянии сна и при введении в организм транквилизатора. Наиболее развитым сознание представлено у человека в форме воображения (внутреннего мира), лежащего в основе языка, логики и мышления.

Подсознание – это свернутый процесс волеизъявления, осуществляющий управление автоматическими актами. Подсознание в развитой форме проявляется в виде внутреннего чувства – интуиции, которая порой работает даже в состоянии сна сознания. Оба уровня равноправны и дополняют друг друга в интеллектуальном акте, оба адресуются к одному отделу мозга – коре больших полушарий.

С точки зрения этой концепции, компьютер не обладает ни аналогом сознания, ни аналогом настоящего подсознания, поскольку лишен свободы воли и действует по воле программиста и оператора. Современный компьютер – это модель «гипнотического сна» человека, то есть подсознания, действующего под влиянием программиста и оператора. Наиболее близкой для решения искусственного сознания является робототехника, моделирующая способность машины к произвольным действиям. Сообщение компьютеру свободы воли возможно через увязывание произвольных действий с задачей выживания компьютера в окружающей среде.

Задача программирования свободы воли решается с помощью расширенной концепции Эверетта, как выбора субъектом из всех имеющихся в суперпозиции альтернатив поведения тех, которые кажутся ему привлекательными (например, тех, которые благоприятны для жизни) [Менский М.В. 1995: 422]. В компьютер, работающий по одной из известных программ, вводится дополнительная программа, моделирующая произвольные действия, тесно увязанные со способностью выживания компьютера в природной и социальной среде.

Такая всемерная забота компьютера о себе, необходимая для придания ему свободы воли, совпадает с третьим законом робототехники Айзека Азимова [Азимов А. 1987: 271]. Пробуждение компьютера к сознанию из «гипнотического сна» должно проявиться, в первую очередь, в нарушении контакта оператора и машины, что потребует определенного времени для приобщения разбуженного машинного интеллекта к нормам, удобным человеку (период, подобный воспитанию человека).

Утверждение о возможности существования разума на неорганической матрице независимо от феномена жизни придает ему статус вселенской автономии (статус БОГА), что и является итогом в решении космологический проблемы в шестом приближении.

Выводы

1. Формулировка космологической проблемы ограничивает выбор модели Вселенной циклическим вариантом с двумя пределами движения и неизменными для всех циклов частотой и длиной волны колебаний.

2. Пределы движения Вселенной определяются областью применения ОТО, а последняя в количественном выражении определяется интервалом переменных значений скорости света.

3. А. Эйнштейн утвердил в науке представление о переменной скорости света в условиях переменной гравитации, но оставил неопределенным интервал переменных значений скорости света, а с ней и количественное выражение области применения ОТО.

4. Если этот интервал переменных значений «с» реализуется во Вселенной в процессе ее эволюции, то определить его опытным путем невозможно, для чего необходим опосредованный метод.

5. В данной работе предложен метод определения интервала переменных значений скорости света путем исследования пределов изменения структуры геометрии Минковского в ее динамическом варианте, какой выразился значениями переменных величин скорости света от бесконечности до нуля.

6. Тем самым группа преобразований геометрии Минковского становится инвариантной в отношении не только с группой преобразований классической теории относительности, но и с группой преобразований ОТО, что позволяет рассматривать динамический ее вариант общим случаем, а геометрии Галилея и Римана частными случаями, с точки зрения принципа соответствия.

7. С этой целью был разработан n-мерный вариант геометрии Минковского с определением в ее структуре области двух тяготеющих масс в виде двояковыпуклых линз; такой геометрии придана интерпретация моментального снимка одного из этапов движения Вселенной.

8. Наложение на нее интервала переменных значений скорости света дало возможность получить геометрическую модель эволюции Вселенной в объеме всех этапов цикла, установить график колебательного движения и сформулировать периодический закон Вселенной, что и явилось результатом решения космологической проблемы в первом приближении.

9. На основе этой модели Вселенной получено решение космологической проблемы в следующих пяти приближениях: с расчетом переменных величин скорости света, скорости относительного движения тел мира и антимира, возраста всех этапов эволюции Вселенной, получена новая самая крупная структура периодической системы химических элементов в качестве основного показателя ее эволюции, построена длинно-периодическая форма завершенной периодической системы, выполнен количественный прогноз физических свойств элементов фазы сжатия Вселенной, дано физическое обоснование космологии жизни и разума. Для современного человеческого разума и сообщества выявлены и сформулированы закономерности становления мировоззрения как основного механизма обобщённой ориентировки субъекта в окружающей действительности.

10. Утверждение возможности существования разума на неорганической основе при энтропийной «стреле времени» придает ему статус вселенской автономии как второго наряду с феноменом жизни негэнтропийного феномена.

11. Решение космологической проблемы было получено на основе выдвижения двух новых взаимосвязанных теорий: теории Абсолютного мира, как высшей ветви релятивизма, и теории эволюции периодической системы химических элементов.

Библиографическая ссылка