Механизм окисления сульфидных компонентов концентрата азотной кислотой существенно различается для различных компонентов сульфидов и зависит преимущественно от состава перерабатываемых материалов. Поэтому правильное понимание его дает возможность создать более рациональную технологию переработки сульфидов металлов и установить условие ведения процесса [1–5].
Математическая модель процесса разложения минералов азотной кислотой определяется уравнением:
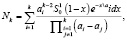 (1)
(1)
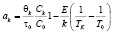 , (2)
, (2)
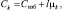
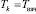 . (3)
. (3)
k=1,2,3, ..., n. (4)
Для решения основного уравнения (1) требуется вычислить интеграл по формуле Симпсона, для чего кинетическую функцию необходимо табулировать при Х=0 1.
1.
Уравнение для безразмерного среднего времени пребывания в каскаде реакторов (2) вычисляется из соотношения 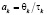 при этом учитываются выражения для
при этом учитываются выражения для 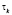 и для q.
и для q.
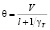 ,
,
где l – объем жидкой фазы, одинаковый для всех ступеней; γT – плотность твердой фазы; ai – безразмерное среднее время пребывания в i-й степени каскада, равное отношению среднего времени пребывания θi ко времени полного растворения τI; bT – стехиометрический расход реагента на единицу массы исходной твердой фазы; С – концентрация (нижние индексы изб. – избыточная); Н – насыщенный раствор (нач. – начальная); n – в периодическом опыте; Е – энергия активации; Yk -рабочий объем k-й степени каскада реактора; X – безразмерное время, равное отношению времени t к времени полного растворения τ (в том числе значения случайной величины, X – безразмерного времени пребывания частицы в каскаде реакторов); α – порядок реакции; γ – плотность (Т – твердая фаза, без индекса – жидкая фаза); μ. – извлечение полезного компонента в раствор; θk – среднее время пребывания в k-й ступени каскада; θs = суммарное среднее время пребывания во всех ступенях каскада; μ – доля не растворившегося компонента в твердой фазе при непрерывном процессе, равная отношению массы не растворившегося компонента к его начальной массе (нижний индекс k на выходе из k-й ступени каскада); τ – время полного растворения (нижние индексы: k – в условиях k-й ступени; 0 – при стандартных значениях температуры Т0 и концентрации С0); W – доля не растворившегося компонента в периодическом процессе; W(x) – кинетическая функция.
Величины, входящие в систему (1)–(4), по смыслу делятся на четыре группы:
– кинетические характеристики процесса: кинетическая функция W(x), равная в нашем случае (1–х)3; время полного растворения то при фиксированных значениях Т0 и С0; энергия активации – Е; порядок реакции – α;
– физико-химические константы: приведенный стехиометрический коэффициент «b»;
– независимые технологические параметры: избыточная концентрация активного реагента Сизб и/или начальная концентрация Снач; начальная температура пульпы Тнач; среднее время пребывания θk в каждой ступени;
– зависимые технологические параметры: μ – доля не растворившегося компонента на выходе каждой ступени; безразмерное среднее время пребывания в каждой ступени; Т – температура; С – концентрация активного реагента.
Величины, входящие в две первые группы, определяются кинетическими характеристиками и физико-химическими свойствами системы; численные их значения – характером процесса. Что же касается параметров, составляющих третью и четвертую группы, то их значения в известных пределах можно менять.
Для решения системы уравнения (1)–(4) в качестве независимого параметра принимаем средне время пребывания θК, а зависимого – долю не растворившегося компонента μ.
Таким образом, основная задача сводится к определению величины извлечения заданного компонента.
В качестве определяемого компонента выбран мышьяк, по остаточному содержанию которого в твердом остатке рассчитывали извлечение в раствор. Программу математической модели системы уравнений (1)–(4) для выщелачивания мышьяка составили на ЭВМ. Исходные независимые технологические параметры процесса выщелачивания мышьяка азотной кислотой из сульфидно-мышьяковых концентрате приводятся в табл. 1.
Для упрощения расчета температуру пульпу (Тнач) и время пребывания концентрата (θ) во всех реакторах приняли постоянными. Долю не растворившегося мышьяка в кеке при разложении сульфидно-мышьякового концентрата азотной кислотой определяли при за параметрах (табл. 1).
Результаты, полученные на ЭВМ, приведены в табл. 2.
Таблица 1
Независимые технологические параметры процесса выщелачивания сульфидно-мышьякового концентрата
|
Параметры |
Обозначения |
Принятые значения |
Область возможных значений |
|
Доля нерастворившегося мышьяка Обьем готового раствора, м3\т |
μn L |
0,01 7,5 |
– 5≤ L≤10 |
|
Температура, К |
Тнач |
333 |
333≤Т≤368 |
|
Концентрация кислоты, г\дм3 |
Сизб |
400 |
300≤Сизб≤500 |
|
Приведенный стехиометрический коэфициент, м3\т (т\т) |
b |
3 |
2≤b≤4 |
Таблица 2
Доля не растворившегося мышьяка в кеке при заданных технологических параметрах процесса
|
Количество ступеней (реакторов) К |
Технологические параметры |
Доля нерастворившегося мышьяка в кеке, μ |
||
|
θ |
Тнач |
а |
||
|
При С0=300 г\дм3 |
||||
|
1 |
30 |
333 |
0,1052 |
0,773 |
|
2 |
30 |
333 |
0,1051 |
0,540 |
|
3 |
30 |
333 |
0,1049 |
0,382 |
|
4 |
30 |
333 |
0,1048 |
0,263 |
|
При С0=400 г/дм3 |
||||
|
1 |
45 |
353 |
0,436 |
0,385 |
|
2 |
45 |
353 |
0,435 |
0,232 |
|
3 |
45 |
353 |
0,435 |
0,04 |
|
4 |
45 |
353 |
0,434 |
0,011 |
|
При С0=500 г/дм3 |
||||
|
1 |
60 |
367 |
1,193 |
0,178 |
|
2 |
60 |
367 |
1,192 |
0,026 |
|
3 |
60 |
367 |
1,191 |
0,003 |
|
4 |
60 |
367 |
1,191 |
0,0004 |
Зависимость доли не растворившегося мышьяка в кеке от количества ступеней (реакторов) при различных концентрациях азотной кислоты и температурах пульпы свидетельствуют о том, что с увеличением концентрации азотной кислоты резко уменьшается количество реакторов. Например, при разложении концентрата азотной кислотой (концентрация 300 г/дм3, начальная температура пульпы 333 К) число реакторов, необходимое для достижения заданной доли не растворившегося мышьяка (μ=0,01), должно быть более четырех; при концентрации азотной кислоты 500 г/дм3 и начальной температуре 367 К достаточно двух реакторов. Следует отметить, что программа, составленная на основании системы уравнений (1)–(4), позволяет с помощью ЭВМ, меняя в известных пределах технологические параметры, определить оптимальные условия процесса. Для этого необходимо предварительно знать кинетические данные изучаемой системы.
Вывод
В работе исследованы кинетические закономерности разложения в растворах азотной кислоты чистых минералов пирита, арсенопирита флот концентрата.
При изучении кинетики взаимодействия пирита и арсенопирита с азотной кислотой найдены величины порядка реакций, определены значения энергии активации реакций окисления. Предложена математическая модель процесса, растворение сульфидных минералов протекающих в диффузионно-кинетической области либо диффузионной области.
На основании кинетических исследований по окислению сульфидных составляющих флот концентратов, а также физико-химических исследований кеков предложен механизм гетерогенного окисления пирита и арсенопирита раствором азотной кислоты.
В результате проведенных исследований определены оптимальные условия вскрытия концентратов: концентрация азотной кислоты с продувкой воздуха 250–460 г/дм3, отношение Т:Ж=1:(5  10). температура 80–95°С и продолжительность выщелачивания 2–3 ч.
10). температура 80–95°С и продолжительность выщелачивания 2–3 ч.
Библиографическая ссылка
Абдула Ж., Галагузова Т.А., Молдыбаева Г., Амиров К. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ПРОЦЕССА РАЗЛОЖЕНИЯ МИНЕРАЛОВ АЗОТНОЙ КИСЛОТОЙ // Международный журнал экспериментального образования. 2016. № 5-2. С. 175-177;URL: https://expeducation.ru/ru/article/view?id=9949 (дата обращения: 06.03.2026).

