Культура принятия решений, т.е. умение находить и логически обосновывать решения, нужна управленцам практически любой отрасли, что требует от них творческого подхода в своей деятельности. Бесспорно, что эффективно творить, т.е. открывать неизведанное, наиболее продуктивно учит математика. Поэтому очевиден вывод: надо повышать математическую культуру старшеклассников и студентов, чтобы решение творческих задач для них стало скорее нормой, чем исключением. Умение логически мыслить является базисной компетенцией, такой же, как умение излагать свои мысли или выделять логические связи в изложении собеседников. Однако именно логическое мышление является основой указанных способностей. Мудрость – это самая точная из наук (Аристотель).
Исходя из насущной необходимости повышения логической культуры учащихся, автором была разработана система «Живая логика», которая является компонентом общей системы «Живая математика», представляющей собой единую среду решения математических задач в объеме средней школы. Описание системы «Живая математика» достаточно подробно представлено в [1], поэтому здесь на этом не останавливаемся. Предназначение «Живой логики» состоит в выработке у старшеклассников и студентов устойчивых навыков логического мышления путем решения задач, требующих выстраивания логических умозаключений в условиях неопределенности. «Живая логика» позволяет переходить от задачи к подзадачам, сохраняя логическое следование основной задачи из совокупности подзадач. В ней, главным образом, реализовано логическое правило разбора случаев. Этот прием особенно нагляден при решении логических и комбинаторных задач, решаемых перебором, требующим анализа вариантов для окончательного решения. Тем самым «Живая логика» автоматизирует процесс разбиения задач на подзадачи, позволяя «на лету» предлагать варианты решения. А наличие автоматической проверки условий, которым должна удовлетворять каждая подзадача, позволяет обнаруживать противоречия и отвергать неверные гипотезы. При этом все рассматриваемые варианты поиска решения сохраняются, что позволяет вернуться к предыдущему варианту и провести его дополнительный анализ.
С технической точки зрения «Живая логика» формирует деревья решений большой глубины при неограниченном ветвлении в каждом узле. Такой разбор вариантов позволяет проследить всю последовательность шагов, приводящих к решению исходной задачи. Если вы интересовались математическими головоломками, решение которых не видно сразу, а требует разбора случаев, то представляете очевидную полезность такого механизма. Например, решение такой головоломки: в сумме

следует подставить разные цифры вместо разных букв, чтобы получилось тождество. Здесь же следует упомянуть широко распространенные логические задачи, например про волка, козу и капусту. При всей простоте формулировки такие задачи требуют от обучающегося логического мышления и правильного построения умозаключений. В школе ввиду отсутствия предмета «Логика» этому не учат. Поэтому на ЕГЭ решение комбинаторных задач считается одним из самых трудных заданий.
При разработке «Живой логики» автор исходил из того, что каждая задача в своей формулировке уже содержит решение. Этот тезис сформулирован и обоснован в [2]. Однако, чтобы это решение увидеть, требуется соответствующая формулировка задачи. Именно это предлагается в «Живой логике». В частности, предлагается формальный язык описания задач: с одной стороны – с содержательной семантикой, а с другой – позволяющий реализовать операционную семантику нахождения решения.
Следует отметить, что предполагаемый круг пользователей подсистемы «Живая логика» достаточно обширный. В первую очередь это преподаватели, намеревающиеся повысить как уровень логического мышления обучающихся, так и эффективность своего труда путем увеличения скорости и наглядности решения логических и комбинаторных задач [3]. Сюда же относятся и репетиторы по математике, которые смогут более эффективно готовить своих подопечных к ЕГЭ. И, конечно, это школьники, готовящиеся к ЕГЭ или олимпиадам по математике и вырабатывающие у себя навыки математического мышления. С этой целью интерфейс системы «Живая логика» ориентирован на контингент пользователей, слабо подготовленных в области ИТ.
Двухуровневый язык описания задач
Описание задачи в системе «Живая логика» осуществляется на формальном языке, который содержит словарь атомарных формул и обычные логические связки: NOT, AND, OR, XOR. Вначале подробно остановимся на атомарных формулах, поскольку именно они позволяют формулировать содержательные единицы задачи.
Первая часть словаря атомарных формул представляет описание возможных инициализаций параметров задачи (аналог инициализации переменных в языках программирования). Ниже перечислены соответствующие конструкции языка и разобраны примеры их конкретного использования.
1.1. Атомарные формулы, определяющие инициализацию переменных. На переменные и присваиваемые им значения особых ограничений не накладывается. Так как изложение в статье ведется на содержательном уровне, то, не вникая в подробности, приведем лишь примеры таких атомарных формул и их содержательные интерпретации: A=12# – переменная A имеет значение 12; Петя=Велосипед# – у Пети есть велосипед; Илья Муромец=Победа над Соловьем-разбойником# – Илья Муромец победил Соловья-разбойника. Характерными чертами таких атомарных формул являются знак равенства и символ # в конце. Аналогия с инициализацией переменных в языках программирования очевидна. Отличие в том, что здесь не учитываются типы данных переменных, как это принято в большинстве языков программирования [4], и одна переменная может инициализироваться несколькими значениями. Например, Петя=5 класс# Петя=Имеет велосипед#, что соответствует высказыванию: Петя учится в пятом классе и у него есть велосипед.
1.2. Линейные зависимости выражаются последовательностью равенств, каждое из которых инициализирует в точности одну переменную единственным значением. Пример: A=1# Bася=машинка# Света=Зеленое платье#. Такая инициализация происходит в случае, когда, например, одновременно выполняются события: переменная A принимает значение 1, у Васи есть машинка и Света пришла в зеленом платье. Используется тогда, когда для переменных A, B, C не существует альтернативных значений.
Пример 1.1. Пусть из условия задачи следует, что переменные A и B связаны равенством: A + 1 = B и переменная A принимает единственное значение – 2. Тогда переменные A и B связаны линейной зависимостью: A=2# B=3#
1.3. Множественные линейные зависимости выражаются последовательностью равенств, каждое из которых представляет возможную инициализацию переменной. Например, А=2,3#B=3,5#C=7,8#. Эта зависимость есть сокращение для нескольких независимых линейных зависимостей: А=2# B=3# C=7# и А=3# B=5# C=8#. Каждая из них представляет собой отдельную подзадачу. Тем самым одной строкой задаются две независимые подзадачи, которые решаются по отдельности.
Пример 1.2. Пусть нам известно, что переменная A может принимать два значения – 2 или 3. И значения переменных B и C однозначно определяются ими. При A = 2 переменные B и C имеют значения соответственно 3, 7, при A= 3 – соответственно 5 и 8. Тогда это легко представляется множественной линейной зависимостью: А=2,3# B=3,5# C=7,8#. Такое представление распространено при решении математических головоломок и комбинаторных задач.
1.4. Атомарные формулы, реализующие множественные инициализации переменных. Например, А={10, 12}# – переменная A может принимать оба значения – 10 и 12; Зина={Джинсы, Платье}# – Зина может надеть джинсы и платье; Богатырь={Илья Муромец, Алеша Попович}# – богатырем может быть как Илья Муромец, так и Алеша Попович.
1.5. Независимость переменных подразумевает, что они могут инициализироваться без соблюдения каких-либо зависимостей. Например, запись A={1,2}# B={3,4}# обозначает, что переменные A и B независимые и могут инициализироваться четырьмя различными способами: A=1#B=3#, A=1#B=4#, A=2#B=3#, A=2#B=4#. Следовательно, одна короткая запись определяет четыре независимые подзадачи. Следует отметить одну особенность языка «Живой логики», которая в настоящее время не имеет места в языках программирования: множественность областей определения одной переменной. Поясним следующим примером. Запись Зина={9, 10}# Зина={Красное платье, Зеленое платье}# может интерпретироваться как: Зина учится либо в 9-м, либо в 10-м классе, а на встречу она пришла либо в красном, либо в зеленом платье. Такое разделение областей определения переменных позволяет существенно упрощать спецификации задач, оставляя главное – их содержательность.
Пример 1. Проиллюстрируем эти методы инициализации переменных на примере ручного решения математической головоломки
 ,
,
в которой надо подставить разные цифры вместо разных букв, решаемой с помощью подсистемы «Живая логика». С целью экономии места не будем приводить снимки экрана. Вместо этого подробно представим последовательность шагов от введения начального условия до окончательного решения. Несколько видео с подробным изложением приемов работы с «Живой логикой» будет выложено на YouTube в канале автора.
1. Введение условия задачи – формулируется содержательная спецификация задачи и в случае необходимости приводится ее графическая интерпретация. Для этого используется подсистема ввода условий задачи. Задача формулируется на содержательном уровне, что требуется для сохранения протокола решения, представимого в содержательных терминах.
2. Следующий этап – начало построения дерева решений, представляющего собой однокорневое растущее вниз дерево. Его корнем является вершина Start, ниже которой будет формироваться все дерево поиска решения.
3. Первый шаг – выбираем значение буквы М. Поскольку в задаче предполагается операция сложения и М является переносом в пятый разряд суммы, то вводим атом M=1# как непосредственный потомок корневой вершины Start. В результате получается новая вершина 2. M=1, которая имеет своим родителем корень дерева Start. В содержательную и графическую части вносим соответствующие изменения, которые будут сохраняться в протоколе решения. Содержательная формулировка задачи приобретает вид
 .
.
Так она сохраняется в протоколе решения.
4. Очевидно, что либо S=8, либо S=9. Поэтому выделяем корень поддерева 2. M=1 и создаем его новые непосредственные потомки, вводя выражение S={8,9}#. Как результат получаем дерево, в котором вершина 2. M=1 обладает двумя непосредственными потоками: 3. S=8 и 4. S=9. Соответствующие изменения в содержательные части вносятся вручную:
 и
и 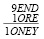 .
.
Они добавляются к протоколу решения.
5. Для продолжения построения решения выбираем вершину 3. S=8. Очевидно, что в этом случае O=0. Чтобы не загромождать изложения, в последующем не будем приводить содержательные иллюстрации возникающих подзадач. Они легко восстанавливаются из приводимых рассуждений. Строим непосредственно ниже вершину дерева 5. O=0. Продолжение решения основывается на таких рассуждениях. Так как по условию задачи E №6. Построение ниже вершины 4. S=9 происходит так же, как в предыдущем случае, т.е. ниже вершины 3. S=8. Вначале инициализируем O=0#, получая вершину 11. O= 0, далее инициализируем переменные E и N, учитывая, что N=E+1. Непосредственными потомками вершины 11. O=0 служат шесть вершин 12–17, определяемых значениями переменных E и N.
7. Просматривая вершины 12–17, убеждаемся, что существует единственное правильное продолжение вершины 15. E=5, N=6 в виде R=8#D=7#Y=2#.
8. Таким образом, в результате рассмотрения решения математической головоломки были продемонстрированы некоторые возможности полуавтоматического формирования зависимостей между компонентами, описывающими задачу. Тем самым «Живая логика» дает возможность наглядно представлять перебор, используемый для решения задач. После нахождения окончательного решения все решение может быть проиллюстрировано, поскольку все его шаги сохранены в протоколе.
Пример 2. Рассмотрим известную задачу про Волка, Козу и Капусту: на правом берегу находятся Волк, Коза, Капуста и лодка с лодочником. Их необходимо перевезти на левый берег в лодке, которая, кроме лодочника, вмещает кого-либо одного: Волка, Козу или Капусту. При этом в отсутствие лодочника Волк может съесть Козу, а Коза – Капусту. Исходная формулировка задачи выглядит Лодочник = Правый берег# Волк = Правый берег# Коза = Правый берег# Капуста = Правый берег#.
Решение задачи выглядит как последовательность умозаключений, характеризующаяся с относительно небольшим перебором. Поэтому оно представляется единственной ветвью из исходного состояния, когда все на правом берегу, до состояния Лодочник = Левый берег# Волк = Левый берег# Коза = Левый берег# Капуста =Левый берег# – все на левом берегу. Каждый переход в дереве от родителя к потомку имеет логическое обоснование. Так из начального состояния можно перейти только в правильное состояние: Лодочник = Левый берег# Волк = Правый берег# Коза = Левый берег# Капуста = Правый берег#. Анализируя промежуточные состояния и устраняя тупики и повторения, получаем кратчайшую последовательность шагов, приводящую к окончательному решению.
Вторая часть словаря атомарных формул подсистемы «Живая логика» предполагает формулировку ограничений, которым должны удовлетворять значения переменных в каждом состоянии поиска решения (или, что то же самое, в вершине дерева поиска).
2.1. Проверка значений переменных на равенство (==) и неравенство (<>) определенным значениям. Так, условие А==3# B<>5# обозначает, что в подзадаче переменная A должна быть равна 3, а переменная B отлична от 5. Формулировка ограничений в подзадачах (они же – вершины дерева поиска решения) позволяет существенно снизить перебор и тем самым – количество возможных продолжений дерева поиска.
2.2. Проверка переменных на взаимное равенство и неравенство. Так, A==B# и A<>B# обозначает соответственно условия равенства и неравенства значений переменных A и B независимо от этих значений. Такие ограничения также направлены на то, чтобы снижать количество возможных продолжений из одной подзадачи.
2.3. Проверка значений переменных на принадлежность множеству значений. Например, A in 1,2,3# обозначает, что в формулируемой подзадаче значение переменной A должно принадлежать множеству {1, 2, 3}.
2.4. Проверка значений переменных на непринадлежность множеству значений. Например, A not in 1,2,3# обозначает, что в формулируемой подзадаче значение переменной A не должно принадлежать множеству {1, 2, 3}.
Пример 3. Рассмотрим формальное представление такого утверждения: У Кати, Оли и Светы три кошки, одна черная и две белые. Известно, что у Кати и у Оли кошки разного цвета, как и у Оли со Светой. Какие кошки у девочек? На языке условий эти высказывания представляются следующим образом: Катя={Белая кошка, Черная кошка}# Оля={Белая кошка, Черная кошка}# Света={Белая кошка, Черная кошка}# Катя<>Оля# Света<>Оля#. Вводя такое условие задачи, получаем решение: у Оли – черная кошка, а у Кати и Светы – белые.
Логический язык управления условиями. Условия, которым должны удовлетворять подзадачи, допускают использование логических связок: NOT, AND, OR, XOR. В результате ограничения представляют собой язык первого порядка с введенными атомарными формулами, конструкции которого не содержат кванторы. В данном случае мы не останавливаемся подробно на семантике этого языка, что требует более глубоких знаний из математической логики. Наша цель – представить общую концепцию «Живой логики» и основы ее использования.
Второй уровень языка описания задач. Следующий уровень языка описания задач предполагает использование пропозициональных связок NOT, AND, OR, XOR с обычной семантикой, принятой в математической логике, и скобок при записи исходной формулировки задачи. Логические выражения формулируются так, как это принято в исчислении первого порядка, в качестве предикатов используются атомарные формулы, представленные выше. Тем самым в «Живой логике» реализована возможность описания задач в виде логических выражений. Так выражение (Валя = Голубое Платье# XOR Витя = Широкополая шляпа AND NOT Витя=Велосипед#) содержательно интерпретируется как утверждение: «Либо Валя была в голубом платье, либо Витя пришел в широкополой шляпе и не на велосипеде». Как показывает опыт решения логических задач, такой язык обладает достаточными выразительными возможностями для описания задач, которые встречаются в школьном курсе при подготовке к ЕГЭ или к олимпиадам по математике [5].
После формулировки задач происходит приведение спецификации задачи к ДНФ, в которой каждый конъюнкт представляет собой отдельную задачу, требующую решения. В наиболее простых случаях конъюнкт, если он не содержит противоречий, уже представляет решение окончательное. Например, из конъюнкции: Галя = Фея# Даша <> Павлин# Аня = Зайчик# Валя <> Фея# Аня <> Фея# Даша=Петух# легко извлекается решение: на карнавале Галя была в костюме феи, Аня – зайчика и Даша – петушка. Эти высказывания согласуется с ограничениями, представленными неравенствами Даша <> Павлин#, Валя <> Фея#, Аня <> Фея#. С учетом ограничений, например неравенства переменных A<>B, можно формулировать более сложные фильтры, оставляющие только решения, не содержащие логических противоречий.
Заключение
Представлена система «Живая логика», предназначенная для автоматизации решения комбинаторных задач, главным образом, из школьного курса. Система представляется полезной для школьных преподавателей математики и информатики, репетиторов и школьников, готовящихся к ЕГЭ или олимпиадам по математике. Опыт использования «Живой логики» показывает, что эффективность выработки навыков логического мышления у обучающихся существенно возрастает.

