Пусть материальная частица располагается на винтовой поверхности спирали, установленной в насыпи и вращающейся относительно оси с угловой скоростью. При движении частица прижимается к внешним слоям и к витку спирали. Нахождение скорости, обуславливающей производительность, связано с определением угловой скорости относительного движения ' при соблюдении условия равновесии из решения системы уравнений [1]:
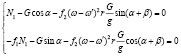 , (1)
, (1)
где G – вертикальная составляющая силы давления частицы на спираль; r – радиус спирали; N2 – сила, соответствующая давлению насыпи на материальную частицу; N1 – давление поверхности спирали; f1 – коэффициент трения о виток спирали; f2 – коэффициент трения о насыпь.
Умножим первое уравнение системы (1) на f1, и сложим его со вторым, сокращая на G получим:
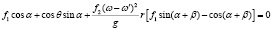 . (2)
. (2)
Положив в уравнении (2) = 0°, cos = 1, sin = 0, условия, при которых подъема частицы не будет, имеем:
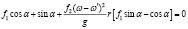 . (3)
. (3)
Отсюда 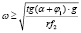 ,
,
где 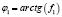 .
.
Следовательно, для движения массы частиц вверх вдоль оси спирали необходимо соблюдение данного условия.
Библиографическая ссылка
Исаев Ю.М., Семашкин Н.М., Джабраилов Т.А., Кошкина А.О., Настин А.А, Хабарова В.В. УСЛОВИЕ ПЕРЕМЕЩЕНИЯ ЧАСТИЦ СПИРАЛЬНЫМ ВИНТОМ В НАСЫПИ // Международный журнал экспериментального образования. 2016. № 11-1. С. 105-106;URL: https://expeducation.ru/ru/article/view?id=10718 (дата обращения: 07.01.2026).

