Научный журнал

Международный журнал экспериментального образования

ISSN 2618–7159

ИФ РИНЦ = 0,425

• Авторы
• Файлы
• Литература

Далингер В.А. 1

---

1 Омский государственный педагогический университет

Статья в формате PDF

2472 KB

1. Бурмистрова Н.А. Математическое моделирование экономических процессов как средство формирования профессиональной компетентности будущих специалистов финансовой сферы при обучении математике: монография. – М.: Логос, 2010. – 228 с.

2. Дмитриева А.Б. Самостоятельная работа по решению прикладных задач в курсе математики как условие повышения качества профессиональной подготовки обучаемых в вузе: автореф….дис. на соиск. уч. степ. канд. пед. наук. – М., 2004. – 19 с.

3. Далингер В.А. Экономическое образование учащихся на уроках математики // Менеджмент в социальных структурах: межвузовский сборник научных трудов. – Омск: Изд-во ОмГПУ, 1999. – С 298-310.

4. Еленкин А.Г. Экономико-прикладная направленность обучения математике: автореф….дис. на соиск. уч. степ. канд. пед. наук. – М., 2000. – 19 с.

5. Картёжникова А.Н. Развитие профессионально важных качеств будущих специалистов экономического профиля в процессе обучения математике: контекстный подход: монография. – Чита: Изд-во НОУ ВПО ЗИП СибУПК, 2013. – 180 с.

6. Новиков П.Н. Задачи с межпредметным содержанием в средних профессионально-технических училищах. – Минск: Вышейша школа, 1987. – 147 с.

7. Шапиро И.М. Использование задач с практическим содержанием в преподавании математики: книга для учителя. – М.: Просвещение, 1990. – 96 с.

В российской системе образовании произошло смещение акцентов с информационно-предметных позиций на личностно-ориентированные, творческо-развивающие. Одна из целей образования на старшей ступени общеобразовательной школы состоит в профессиональном самоопределении учащихся.

В настоящее время обнаруживается дефицит в специалистах, обладающих знаниями, умениями и опытом действия в условиях развивающихся рыночных отношений. Нужны специалисты для финансово-экономической сферы деятельности.

Математика обладает большими потенциальными возможностями для формирования у учащихся интереса к профессиям, связанных с указанной сферой деятельности.

Одним из таких средств являются прикладные математические задачи с экономическим содержанием. Эти задачи направлены на:

– мотивирование школьников на изучение экономических приложений математики;

– формирование умений решать прикладные задачи;

– расширение межпредметных связей;

– обучение математическому моделированию экономических процессов и явлений;

– развитие творческой активности учащихся;

– направленность обучения математике на выбор профессии из финансово-экономической сферы деятельности.

П.Н. Новиков отмечает: «Если содержание специально подобранных задач связано с открытием существенных элементов мастерства в той или иной профессии, то такие… задачи становятся средством формирования интереса к профессии» [6, с. 56].

Мы, следуя А.Б. Дмитриевой, будем под прикладной задачей понимать «задачу, описывающая реальную или приближенную к реальной ситуацию и решаемая математическими методами» [2, с. 13].

А.Н. Картежникова [5] предлагает рассматривать прикладные задачи экономического содержания двух видов:

1) математические задачи с экономическим наполнением, направленные на формирование основных математических понятий, а также умений и навыков решения типичных математических задач. Такие задачи подчинены структуре: экономика → математика;

2) экономические задачи, при решении которых используются математические методы. Эти задачи подчинены структуре:

математика → экономика.

Приведем примеры таких видов задач по различным разделам математики.

I. Элементы линейной алгебры

Матрицы и операции над ними

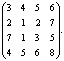
1. Предприятие производит мебель трех видов и продает её в четырех регионах. Матрица

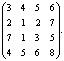
задает цену реализации единицы мебели i-го типа в j-м регионе. Определите выручку предприятия в каждом регионе, если реализация мебели за месяц (по видам) задана матрицей

2. Предприятие выпускает четыре вида изделий с использованием четырех видов сырья. Нормы расхода сырья представлены матрицей

Необходимо определить затраты сырья для производства каждого вида изделий, если план выпуска продукции задан матрицей-строкой .

Уравнения и системы линейных уравнений

1. Фирмой было выделено 236 тыс. у. е. на покупку 29 предметов для оборудования офиса: нескольких компьютеров по цене 20 тыс. у. е. за компьютер, офисных столов по 8,5 тыс. у. е. за стол, стульев по 1,5 тыс. у. е. за стул. Позже выяснилось, что в другом месте компьютеры можно приобрести по 19,5 тыс. у.е., а столы по 8 тыс. у.е. (стулья по той же цене), благодаря чему на ту же сумму было куплено на 1 стол больше. Выясните, какое количество единиц каждого вида оборудования было приобретено.

2. Штат больницы состоит из 6 санитарок, 8 медсестер, 10 врачей, 3 заведующих отделениями, главный врач, заведующий аптекой, заведующий хозяйством и заведующий больницей. Общий месячный фонд заработной платы составляет 400 тыс. руб. Известно, что медсестра получает в 1,5 раза больше санитарки, врач – в 3 раза больше санитарки, заведующий отделением – на 1300 рублей больше, чем врач, заведующий аптекой – в 2,5 раза больше санитарки, заведующий хозяйством – на 1500 рублей больше медсестры, главный врач – в 4,5 раза больше санитарки, заведующий больницей – на 1500 рублей больше главного врача. Определите какими должны быть оклады сотрудников больницы.

II. Элементы аналитической геометрии

Векторы на плоскости и в пространстве

1. Предприятие выпускает четыре вида продукции в количествах 60, 70, 10, 140 единиц. При этом нормы расхода сырья составляют соответственно 6; 4,5; 12; 5 кг. Определите суммарный расход сырья и его изменение при изменениях выпуска продукции <<dali6.wmf>> соответственно, на +5; –4; –2; +10 единиц.

2. Коммерческий банк, участвующий в строительстве многоэтажных автостоянок в центре Москвы, получил согласие на выдачу кредитов у трех банков. Каждый из них предоставит кредиты в размере 20, 40, 40 млрд. рублей под годовой процент 40 %, 25 %, 30 % соответственно. Определите общую сумму выплат кредиторам.

Прямая на плоскости. Прямая и плоскость в пространстве

1. Издержки производства на 200 единиц продукции составляют 100 рублей, а на 1800 единиц – 700 рублей. Определите графическим способом издержки на производство 600, 1000, 1400 единиц продукции, считая, что функция издержек является линейной.

2. Известны линейные зависимости спроса и предложения от цены товара p. Найдите равновесную цену и выручку от продажи товара при равновесной цене.

III. Введение в исследование операций

Элементы линейного программирования

1. Коммерческий банк имеет на три месяца свободные денежные ресурсы в количестве 1 млдр. рублей. Доходность от вложения в ценные бумаги составляет 29 %, в то время как на межбанковском рынке можно получить 17 % прибыли, а вложения в валюту с последующей конвертацией обеспечит лишь 14 %. Определите максимальный доход от размещения свободных денежных средств.

2. Для производства кирпича двух марок
(I, II) предприятие использует оборудование трех видов (A, B, C), имеющееся в количествах соответственно не более 13, 9, 8 у.е. Для производства одного кирпича I типа требуется 2 у.е. оборудования вида А, 1 у.е. – вида В, 2 у.е. – вида С; для производства одного кирпича II типа – 2, 3, 1 у.е. Известно, что от реализации одного кирпича I типа прибыль составляет 3ден. ед.; II типа – 4 ден. ед. Определите максимальную прибыль.

Элементы теории игр

1. Туристическая фирма планирует организацию продажи туристических путевок в три страны. Спрос на путевки зависит от обстановке в каждой из стран и может принимать одно из двух состояний. В зависимости от этого доход, получаемый фирмой в ближайший месяц, определяет матрица

Необходимо определить соотношение объемов реализации путевок, при котором фирме гарантируется максимально возможная прибыль.

2. Торговая фирма разработала несколько вариантов плана продажи товара на ярмарке с учетом изменений конъюнктуры рынка (спроса покупателей). Полученные при этом экономические показатели представлены матрицей

Определите оптимальный план продажи товара.

IV. Элементы математического анализа

Последовательности и ряды

1. Вклад положен в Сбербанк из расчета 5 % в год. Найдите сумму, которая получится по истечении 25 лет, если начальный вклад – 1000 рублей.

2. Докажите, что заниженный курс рубля выгоден российским импортерам, а завышенный – российским экспортерам. Кому выгоден фиксированный курс рубля при инфляции в России (импортерам или экспортерам)?

Дифференциальное исчисление

1. Функция издержек имеет вид

На начальном этапе фирма организует производство так, чтобы минимизировать средние издержки . В дальнейшем на товар устанавливается цена, равная 4 у.е. за единицу. На сколько единиц товара фирме следует увеличить выпуск?

2. Зависимость между спросом q и ценой p за единицу продукции, выпускаемой некоторым предприятием, выдается соотношением . Выясните, при каких значениях цены спрос является эластичным, нейтральным, неэластичным. Какие рекомендации о цене за единицу продукции можно дать руководителям предприятия при p=100, p=150 денежных единиц?

Функции нескольких переменных

1. Производственная функция имеет вид , где x – количество единиц первого ресурса, y – второго. Стоимость единицы первого ресурса 8 ден. ед., единицы второго – 4 ден. ед. В силу бюджетных ограничений на приобретение ресурсов может быть потрачена сумма не более 54 ден. ед.. Определите оптимальное потребление x и y.

2. Бизнесмен решил основать небольшое автотранспортное предприятие по оказанию услуг населению. Ознакомившись со статистикой, он увидел, что примерная зависимость ежедневной выручки от числа автомашин А и числа рабочих N выражается формулой . Амортизационные и другие ежедневные расходы на одну машину равны 2400 рублей, ежедневная зарплата сотрудника 3100 рублей. Найдите оптимальную численность рабочих и автомашин.

Интегральное исчисление

1. Найдите объем выпуска продукции за первые 5 часов работы при производительности , где t – время в часах.

2. Изменения производительности производства с течением времени от начала внедрения нового технологического процесса задается функцией , где t – время в месяцах. Найдите объем продукции, произведенной: а) за первый месяц; б) за третий месяц; в) за последний месяц года, считая от начала внедрения рассматриваемого технологического процесса.

Дифференциальные уравнения

1. Функция спроса и предложения на товар имеют вид , . Найдите зависимость равновесной цены p от времени t, если в начальный момент времени () цена составляет 20 ден. ед. Постройте график функции . Определите, является ли равновесная цена устойчивой.

2. Скорость обесценивания оборудования вследствие его износа пропорциональна в каждый момент времени его фактической стоимости. Начальная стоимость . Какова будет стоимость оборудования по истечении t лет?

V. Элементы теории вероятностей

1. Банк имеет 6 отделений. С вероятностью 0,2 независимо от других каждое отделение может заказать на завтра крупную сумму денег. В конце рабочего дня один из вице-президентов банков знакомится с поступившими заявками. Какова вероятность того, что будет: а) ровно 2 заявки; б) хотя бы одна. Какова вероятность того, что есть заявка от первого отделения, если поступило 2 заявки.

2. Банкомат выдает стандартные суммы в 50 рублей, 100 рублей, 500 рублей, 1000 рублей, причем последние составляют лишь 20 %, а первые 60 % всех выдач. В сутки банкомат осуществляет примерно 100 выдач. Сколько же рублей надо заложить в банкомат утром, чтобы до следующего утра их хватило с вероятностью, не меньшей 0,9?

Библиографическая ссылка