Introduction. The organizational and technological level of modern industrial enterprises is largely determined by the creation and application of effective mechanisms for the formation and implementation of strategic plans for the development and effectiveness of the operational management of all production, logistics and organizational processes that aim to achieve high profitability, development and improvement of production. Therefore, the construction of the organizational structure of enterprise management is a complex multi-level problem [1–15]. Principles and methods of the construction of organizational management structure are directly dependent on many factors. The most significant of these are the specifics of the particular production process the set of technological processes used, production volume, productive capacities used, tactical, technical and quality parameters of the products, the issues of standardization and certification, the qualification level of technical, administrative and management personnel, the management system utilized, the regulatory and legal framework of the enterprise and the organization of internal and external documents. The task of building the organizational structure in an industrial environment is a high-priority task in relation to other problems of industrial process control. Formulation and solution of this problem at a high scientificand technical level is a prerequisite for the effective organization of production, the output of highly competitive products ,the growth of financial and economic indicators, dynamic development and continuous improvement of production.
The relevance of the topic is determined by the need to optimize the organizational structure of the enterprise management as the problem of the «upperlevel» to be the priority decisions as a basic component of a successful and efficient operationofany industrial enterprise, regardless of the type of products and production capacity.
Formation mechanisms of the business game scenarios
Let’s consider the mechanisms of the formation of scenarios that have software support in the workbench «SOTA». The general case of organizational and structural medium of multirole BSG is shown in Fig. 1, where
G – multirole business game (MBG);
Rj – roles in G; 1 ≤ j ≤ NR, where NR – number of roles in G;
gi – samples of G; 1 ≤ i ≤ Ng, где Ng – number of samples of G;
rijk – samples of roles in the samples of G; 1 ≤ i ≤ NRj, where NRj – number of samples of the role Rj.
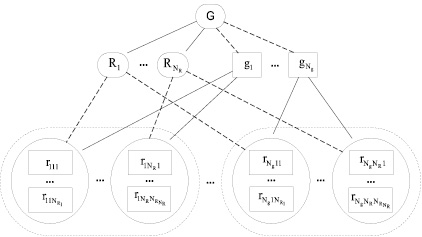
Fig. 1. General case of the organizational structure of the multipart BSG environment
The structure of the individual single-sample BSG which has the possibility to create several interconnected samples of its single role is analogous to the individual BSG with the only sample of this role but supporting several interacting samples of the game [1, 2, 6, 8]. Broken lines indicate the class-sample relationships. Arrows indicate relationships of belonging. Various versions of the organization of the management flow are possible when developing the body of BSG (Fig. 2). Octagons denote syncing fragments.
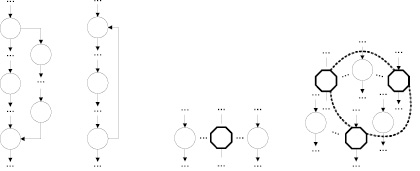
a b c d
Fig. 2. Options of the flow control
Performance of the BSG frame is defined by the following parameters (their values are set during the developmental stage of the game): whether it is single or multipart; there is limitation in the choice of roles.
Schematically, the process of creating a new multirole BSG on the basis of the framework and using the developed tools can be represented by the diagram on Fig. 3. Typically, the BSG scenario then consists of the main part and auxiliary part.
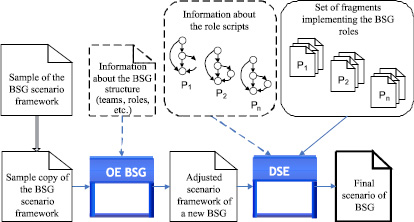
Fig. 3. New BSG creation process
The auxiliary part represents a universal frame work that implements initialization and de-initialization functions common to a large class of BSGs. These functions are preparatory for the formation of the organizational structure of the BSG in accordance with limitations introduced at the developmental stage and are responsible for the dissolution of the BSG. The organizational and structural environment created during the BSG forms as a result of registration of participants of the game.
The BSG framework consists of the following four elements:
● Initialization part:
1) F1 – creation of the new BSG sample (new gaming group) or choosing the existing one (choosing the group);
2) F2 – choosing a role from the list of roles provided in the BSG, creation of the sample (joining the group in the quality defined by the chosen role);
3) F3 – waiting for the selection of the other compulsory available roles (the number for each role has a predefined number of samples) by the remaining participants of the game. Any participant registered in the given sample of the game can initiate the game if the conditions below are satisfied:
a) There are BSG roles assuming an arbitrary number of samples;
b) All the compulsory roles with the predefined number of samples are occupied in all the current BSG samples.
If a new participant of the game started registering in at least one of the samples of the BSG and has not finished the registration yet, the initiation of the game can temporarily be blocked even if all the above-mentioned conditions are met. Once all the participants are registered the game can be initiated by any of the participants. This fragment of the game is syncs the game.
● De-initialization part:
1) F4 – completion of the role sample. If this was the last incomplete sample of the role among all the samples of roles connected to the given sample of BSG then the completion of this BSG sample takes place. This fragment of the game is non-visual.
Formal approach to the automation of the business game development process
The proposed principles of BSG can partially automate the process of developing new games. This can be done through the usage of a quick scenario assembling designers, parameter adjustment of the template frame of the BSG, storing of the most commonly executed fragment sand their re-use, the availability of means to integrate with mathematical packages – the latter can be used to realize particular aspects of a scenario.
It is possible to estimate the qualifications of the personnel based on the results of the game on the basis of the proposed interactive gaming model. It allows the calculation of the time required to make decisions regarding the management of the production processes.
This work solves the distribution of the personnel and assignment of a particular task problem directed at improving the time parameters of the technological process through variation of the number and time characteristics of human resources in the simulation model associated with each operation in the technological process.
Thus, the random elements aij of the matrix of responses A are indicative of the successful execution of the task at thejth level of BSG by the ith participant, that is
(1)
Probabilities of possible values of aij in the main logistical Rasch model are described by the success function
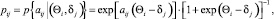(2)
where the level of readiness Θi of the i the participant and the complexity level δj of the task j are parameters which can be evaluated; i = 1, 2, ...n ; j = 1, 2, ...k.
The likelihood function L of a discrete random variable aij is a function of the arguments Θi, δj as the product of the probabilities (2) for all possible values of i and j:
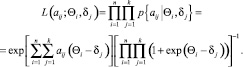(3)
The values of latent parameters 
, 
at which the likelihood function (3) reaches the maximum (we are talking about the global maximum and not the local one here) are taken as the point estimate of the latent parameters. These estimates of 
and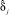 
are called the highest likelihood estimates.
Since the functions L and ln L reach a maximum at the same values of their arguments, instead of looking for the maximum of L, one can look for the maximum of the log-likelihood function lnL
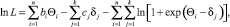(4)
where 
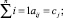
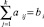(5)
are initial scores of the participants and levels of BSG respectively.
It has been shown that the log-likelihood function depends on the primary scores bi and cj only, which are sufficient statistics (5) of the initial observations (1).
Extremum of the functionis achieved only at the critical points, so we can look at the partialderivatives of the function (8) for each of its arguments
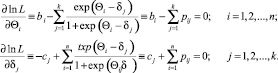(6)
The system of equations (6) represents a system of equations of likelihood. It is nonlinear and contains n + k equations with n + k unknown latent parameters Θi, ...,Θn, δ1,...,δk.
This work demonstrates that the system (6) has only one solution which corresponds to the maximum of log-likelihood function.
Conclusion
In conclusion, the principles of the scenario construction and instruments of the BSG were developed. We proposed network models of the technological processes that form the basis of the description of the interactive simulation scenario and allow us to check the correctness of the scenario, to see the presence of dead-ends and blocks in its description. Also they allow us to identify possible options of the development of the simulated technological process at the early stages of the game.
It was shown that it is possible to transform formal description schemes of the technological processes into a multipart BSG scenario automatically similar to the usage of the critical sections based on the blocking variables during the syncing of the flows of a single process.
The work is submitted to the International Scientific Conference «New technologies in education», Indonesia (Bali), February, 17-25, 2014, came to the editorial office оn 12.12.2013.
Библиографическая ссылка
Ostroukh A.V., Barinov K.A., Surkova N.E. Computer scenarios of business games for personnel training at industrial enterprises // Международный журнал экспериментального образования. – 2014. – № 2. – С. 79-83;URL: https://expeducation.ru/ru/article/view?id=4632 (дата обращения: 21.11.2024).