Совершенствование учебного процесса идет сегодня в направлении увеличения активных методов обучения, обеспечивающих глубокое проникновение учащимися в сущность изучаемой проблемы, повышающих их интерес к учению. К таким методам можно отнести: метод проектов, кейс-метод, учебно-исследовательский метод и т.д.
Проводя учебные исследования, учащиеся осуществляют самостоятельный поиск знаний, испытывают увлеченность идеей и процессом учения; этот вид деятельности реализует познавательную самостоятельность и творческую активность обучающихся.
К чертам творческой деятельности личности можно отнести: логическое мышление, чувство новизны, целенаправленность действий, лаконизм, способность рассматривать явления и процессы с новых точек зрения, и сближать отдельные области знаний, полноценность аргументации, способность чувствовать нечеткость рассуждений и т.д.
А.Н. Колмогоров отмечал, что «даже простейшие математические сведения могут применяться умело с пользой только в том случае, если они усвоены творчески, так что учащийся видит сам, как можно было бы прийти к ним самостоятельно» [5, с. 3].
Под учебным исследованием будем понимать такую деятельность обучающихся, которая осуществляется не по заранее заданному алгоритму, а на основе самоорганизации, способности самостоятельно планировать свою деятельность, осуществлять самоконтроль, перестройку своих действий в зависимости от возникшей ситуации, способность пересмотреть, и, если необходимо, изменить свои представления об объектах, включенных в деятельность.
Практика показывает, что нужно создавать условия, способствующие возникновению у учащихся познавательной потребности в приобретении знаний, овладении способами их использования и влияющие на формирование умений и навыков творческой деятельности.
Успех учебно-исследовательской деятельности учащихся в основном обеспечивается правильным планированием видов и форм заданий, использованием эффективных систем заданий, а также умелым руководством учителем этой деятельностью.
Учитель должен выступать не столько в роли интерпретатора науки и носителя информации, сколько умелым организатором систематической самостоятельной поисковой деятельности учащихся по получению знаний, приобретению умений и навыков и овладению способами умственной деятельности.
В процессе учебных исследований учащиеся овладевают некоторыми навыками наблюдения, экспериментирования, сопоставления и обобщения фактов, делают определенные выводы.
Мотивом учебного исследования может служить интерес, внутреннее противоречие, вызывающее потребность, стремление школьника к исследованию неопределенности, содержащей знания, неизвестные учащемуся.
Приведем примеры заданий, решение которых предполагает проведение учебных исследований и, в конечном счете, направленных на овладение учащимися творческой деятельностью.
I. Задачи с параметрами
Задача 1. Решите уравнения с параметрами:
а)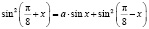 
;
б)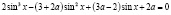 
;
в)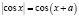 
.
Задача 2. Найдите все значения параметра а, для каждого из которых данное уравнение не имеет корней на указанном промежутке:
а)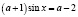 
, 
;
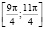б)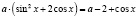 
, 
.
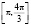Задача 3. Решите неравенства с параметрами:
а)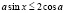 
;
б)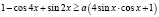 
;
в)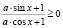 
.
Задача 4. Найдите все значения параметра а, для каждого из которых имеет место данное равенство:
а)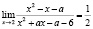 
;
б)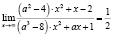 
;
в)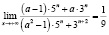 
;
г)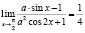 
;
д)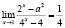 
;
е)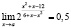 
;
ж)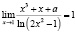 
;
з)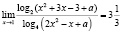 
.
Задача 5. Найдите все значения параметров а и b, при которых парабола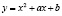 
проходит через точку 
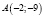и касается прямой 
.
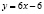Задача 6. Найдите все значения параметра а, при каждом из которых данные неравенства равносильны:
а)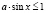 
, 
;
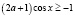б)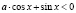 
, 
;
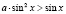в)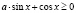 
,
.
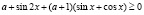Задача 7. Найдите все значения параметра а, при каждом из которых данные уравнения равносильны на данном промежутке:
а)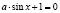 
, 
, 
;
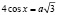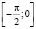б)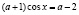 
, 
, 
.
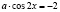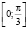Задача 8. Найдите все значения параметра а, при каждом из которых данные неравенства равносильны на данном промежутке:
а)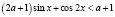 
,
, 
;
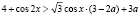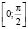б)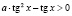 
, 
, 
.
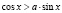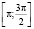Задача 9. Найдите все значения параметра а, при каждом из которых данная функция является непрерывной на всей оси:
а)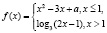 
;
б)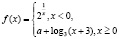 
.
Задача 10. Найдите все значения параметра а, при каждом из которых множество решений одного из данных неравенств содержится во множестве решений другого:
а)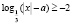 
, 
;
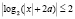б)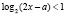 
, 
.
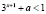Задача 11. Найдите все такие значения а, что площадь, ограниченная линиями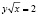 
, 
, 
, 
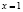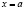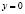, вдвое меньше, чем площадь, ограниченная линиями 
, 
, 
, 
.
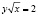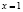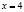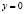Задача 12. При каком значении а, прямая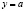 
делит площадь фигуры, ограниченной линиями 
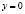и 
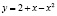, пополам?
Задача 13. Найдите коэффициенты а и b у функции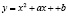 
, если известно, что ее график касается прямой 
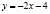и площадь, ограниченная графиком 
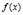и прямой 
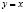, равна 
.
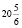II. Арифметические прогрессии с переменной разностью
В школьном курсе математики рассматриваются лишь арифметические прогрессии с постоянными разностями. Напомним читателю определение такой прогрессии.
Арифметической прогрессией называется числовая последовательность, каждый член которой, начиная со второго, равен предыдущему члену, сложенному с одним и тем же числом d, называемым разностью.
Заметим, что из определения следует, что d = const. Можно же сделать так, чтобы разность арифметической прогрессии сама была бы функцией натурального аргумента, то есть dn = d(n). В таком случае мы будем иметь дело с арифметическими прогрессиями с переменными разностями.
Как оказалось, многие известные последовательности являются арифметическими прогрессиями с переменной разностью. Например, фигурные и пирамидальные числа, последовательности степеней натурального ряда ( 1n, 2n, 3n, ... ), показательные последовательности, некоторые возвратные последовательности.
Арифметические последовательности с переменной разностью образуют достаточно широкий класс последовательностей. Имеет место следующий факт: в случае, когда закон изменения разности dn задается произвольно, последовательность частичных сумм любой последовательности есть не что иное, как арифметическая прогрессия с переменной разностью. Получается довольно общая ситуация.
Учащимся следует вначале предложить рассмотреть случай арифметической прогрессии с разностью, заданной рациональной функцией, например: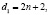 
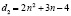. К числу таких последовательностей относятся, например, фигурные и пирамидальные числа, степенные последовательности натуральных чисел и т.д. Учащимся предстоит выяснить какова формула n-го члена соответствующей арифметической прогрессии, сумму n первых членов соответствующей арифметической прогрессии (предположим, что первый член прогрессии равен 1).
Затем следует рассмотреть случаи, когда разность прогрессии задана более сложной формулой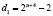 
, 
.
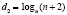Вопросы, связанные с рассмотрением свойств арифметических прогрессий с переменным знаменателем, изменяющимся по рациональному и не по рациональному законам, арифметические прогрессии с переменными разностями порядка выше третьего, связь арифметических прогрессий с многоугольными и пирамидальными числами, вычисление с помощью прогрессий суммы конечного числа степеней натурального ряда и т. д., могут служить благодатным подспорьем в подготовке учащихся к выступлениям с докладами на конференции научных обществ школьников, причем эти доклады будут носить не реферативный характер, что сегодня имеет место в абсолютном большинстве случаев, а творческий, исследовательский.
В нашей литературе [3, 4] читатель найдет обстоятельный разговор о задачах с параметрами и о арифметических прогрессиях с переменными разностями.
Библиографическая ссылка
Далингер В.А. УЧЕБНЫЕ ИССЛЕДОВАНИЯ ПО МАТЕМАТИКЕ КАК СРЕДСТВО ОВЛАДЕНИЯ УЧАЩИМИСЯ ТВОРЧЕСКОЙ ДЕЯТЕЛЬНОСТЬЮ // Международный журнал экспериментального образования. – 2014. – № 3-2. – С. 142-144;URL: https://expeducation.ru/ru/article/view?id=4866 (дата обращения: 21.11.2024).