Введение
Класс задач управления, к которым обычно применяют принцип максимума Понтрягина и динамического программирования (метод Беллмана) являются задачи исследования типа:
• «хищник – жертва»;
• Футболист, догоняющий противника с мячом;
• Преследование подводной лодки надводным кораблем;
• Ракета, догоняющая цель и т.д.
Эти задачи имеют два переменных управления U, V. Целью U минимизация показателя качества, V максимизация этого же показателя.
Перечисленные выше задачи преследования обычно рассматриваются в теории дифференциальных игр [1].
Цель настоящей работы состоит в реализации нечеткого аналога одного из типов четких дифференциальных игр.
Постановка задачи
Имеется модель объекта управления в векторной форме:
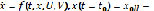
нечеткая переменная с заданной функцией принадлежности 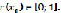 и функционал качества управления (план игры):
и функционал качества управления (план игры):
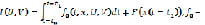
интегрант функционала.
Цель 1-го игрока найти

а цель 2-го игрока – найти
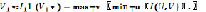
В этих условиях необходимо найти:
1. 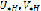 – нечеткое оптимальное управление.
– нечеткое оптимальное управление.
2. Нечеткую цену игры 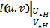 .
.
Отметим здесь, что в четкой задаче имеем 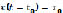 – четкая переменная, а в нечеткой задаче –
– четкая переменная, а в нечеткой задаче – 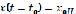 – нечеткая переменная.
– нечеткая переменная.
Метод решения
Алгоритм решения состоит из следующих процедур [1]:
1. Составляется гамильтониан:
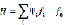 ,
,
где f0 – интегрант функционала; fi – правая модели объекта; ψi – вспомогательная переменная.
2. Находится минимакс Н по переменным 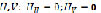 и находятся соответствующие решения
и находятся соответствующие решения 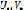 .
.
3. Составляется и решается система канонических уравнений с краевыми условиями:
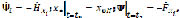
где F(∙) – вторая составляющая функционала качества.
Пример
Решение задачи демонстрируется на примере. Имеем:
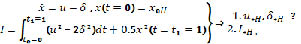
Гамильтониан равен:
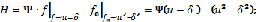
минимакс Н по
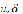 :
: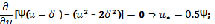
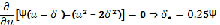 ;
;
каноническая система имеет вид:
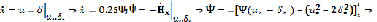
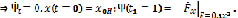
В результате из
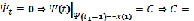 ,
,
откуда
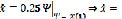
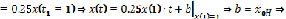
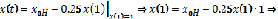
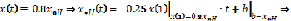
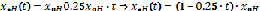
– оптимальная нечеткая траектория в виде нечеткой линейной системы 1 (НЛС)1 относительно 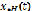 .
.
Далее находим оптимальные нечеткие управления:
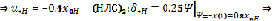
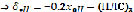 .
.
Нечеткая цена игры равна:
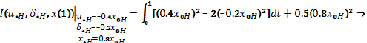
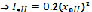 – (НЛС)4.
– (НЛС)4.
В результате получены совокупность (НЛС)I, i = 1,4, каждая из которых решается стандартным способом [2]. Например, для (НЛС)2 имеем расширенную НЛС:
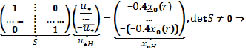
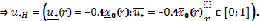
Здесь х0H – нечеткое число, поэтому 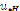 – нечеткая «сильная» переменная.
– нечеткая «сильная» переменная.
Аналогичным способом решаются (НЛС)1,3,4. В результате получим:
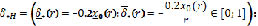
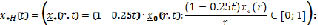
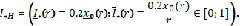
где 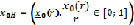 – нечеткое начальное условие с заданной функцией принадлежностей r(x0), r ∈ [0;1], x0 ∈ R1.
– нечеткое начальное условие с заданной функцией принадлежностей r(x0), r ∈ [0;1], x0 ∈ R1.
Полученные нечеткие решения зависят только от х0H, которое является нечетким числом, поэтому все полученные решения являются «сильными» решениями.
ВЫВОДЫ
1. Сформулирована нечеткая игровая задача, которая решается традиционным методом с последующей фазификацией полученного решения.
2. На простейшем примере показана методика нечеткого решения игровой задачи. Показано, что все получаемые нечеткие решения являются «сильными».
Библиографическая ссылка
Мочалов И.А., Хрисат М.С. НЕЧЕТКИЕ ЗАДАЧИ ИССЛЕДОВАНИЯ ДИФФЕРЕНЦИАЛЬНЫХ ИГР // Международный журнал экспериментального образования. 2014. № 8-2. С. 74-76;URL: https://expeducation.ru/ru/article/view?id=5885 (дата обращения: 12.03.2026).

