Научный журнал

Международный журнал экспериментального образования

ISSN 2618–7159

ИФ РИНЦ = 0,425

• Авторы
• Файлы
• Литература

Федоров А.Я. 1 Мелентьева Т.А. 2 Мелентьева М.А. 3

---

1 Тульский институт управления и бизнеса им. Н.Д. Демидова

2 Тульский педагогический университет им. Л.Н. Толстого

3 Российская академия музыки им. Гнесиных

Статья в формате PDF

2255 KB

1. Опойцев В.И. Равновесие и устойчивость в моделях коллективного поведения. – М.: Изд-во «Наука», 1977. – С. 3–5.

2. Карлин С. Математические методы в теории игр, программирование в экономике. – М.: Изд-во «Мир», 1964. – 324 с.

3. Марищима М. Равновесие, устойчивость, рост. – М.: Изд-во «Наука». 1972. – 423 с.

4. Никайдо Х. Выпуклые структуры и математическая экономика. – М.: Изд-во «Мир». 1972. – 228 с.

5. Варшавский В.И. Коллективное поведение автоматов. – М.: Изд-во «Наука». 1973. – 426 с.

6. Федоров А.Я., Мелентьева Т.А., Мелентьева М.А. Экономические закономерности туристского рынка. – Т.: Изд-во «Папирус». «Актуальные тенденции в экономике, управлении, образовании: современный взгляд», 2014. – С. 123–125.

7. Федоров А.Я., Мелентьева Т.А., Мелентьева М.А. Моделирование экономических закономерностей туристского рынка. – Т.: Изд-во «Папирус». «Демидовские чтения – Тула, 2014: экономика и образование». 2014. – С. 318–320.

8. Динамическая теория биологический популяций. Под ред. Р.А. Полуэктового. – М.: Изд-во «Наука». 1974. – 342 с.

9. Свирежев Ю.М., Елизаров Е.Я. Математическое моделирование биологических систем. – М.: Изд-во «Наука». «Проблемы космической биологии», 1972. – Т. 20. – 211 с.

10. Квартальнов В.А. Туризм. – М.: Изд-во «Финансы и статистика», 2002. – С. 168–174.

11. Гуляев В.Г. Туристские перевозки. – М.: Изд-во «Финансы и статистика», 1998. – 143 с.

12. Козырев В.М. Основы современной экономики. – М.: Изд-во «Финансы и статистика», 1998. – 243 с.

13. Бережная Е.В., Бережной В.И. Математические методы моделирования экономических систем. – М.: Изд-во «Финансы и статистика»,2001. – С. 157–158.

14. Вентцель Е.С., Овчаров Л.А. Прикладные задачи теории вероятностей. – М.: Изд-во «Радио и связь», 1983. – 415 с.

15. Гнеденко Б.И., Беляев Ю.А., Соловьев А.Д. Математические методы в теории надежности. – М.: Изд-во «Наука», 1962. – 524 с.

Последующее изложение посвящено задаче описания функционирования системы в целом на основе заданных алгоритмов поведения ее отдельных элементов [1]. Эта задача весьма широко распространена. В этом плане можно интерпретировать даже изучение системы обыкновенных дифференциальных уравнений:

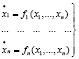, (1)

где xi – переменная, fn – дискретная функция. Переменной xi распоряжается некий (фиктивный) элемент Аi, алгоритмом поведения которого является 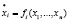. Именно в подобном математическом выражении (1) изучаются поведенческие модели в экономике [2, 3, 4], ряд задач коллективного поведения автоматов [5], динамики популяций в биологии [6, 7] и т.д. Часто в экономике рассматривается модели туристского рынка и сосуществования биологических видов.

Вся классическая наука исходит из того, что одним из основных законов рынка является закон стоимости, который действует и на туристском рынке. Закон стоимости предполагает формирование у каждой отдельной туристской фирмы индивидуальных затрат труда и ресурсов и соответственно формирование индивидуальной стоимости и индивидуальных цен на турпродукт, однако рынок признает не эти индивидуальные стоимости и цены, а общественные и рыночные, в основе которых лежит общественно необходимые затраты труда (ОНЗТ). Помимо ОНЗТ на стоимости и цены оказывают влияние и другие факторы, например, внутри отраслевая конкуренция [8–9].

Российская экономика имеет свои особенности. У нас, к сожалению, при повышении цены на товары, в общем, и туристский продукт, в частности, предложение не увеличивается, а, наоборот снижается. Это явление получило название «российский парадокс». Кризис августа 1998 г. повлек за собой в среднем трехкратное повышение цен, в то же время он разорил многих предпринимателей и сократил предложение туристского продукта (таблица).

Зависимость стоимости тура в Испанию от спроса

Для развития туристской отрасли, в общем, и туристских фирм в частности важно знать темпы изменения трех экономических величин: цены, спроса и предложения. В этом помогает такое понятие, как «эластичность спроса» [10].

Коэффициент эластичности спроса по цене рассчитывается по формуле:

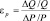, (2)

где DQ – процент роста объема покупаемого товара Q; DP – процент падения цены P. Рассчитаем ценовую эластичность спроса при линейной зависимости стоимости тура от спроса (2) на путешествия в Испанию 1998 г. и различных уровнях цен:

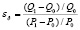, (3)

где индексы 1 и 0 означают соответственно новые и базовые цены и количество проданных туров. С использованием (3) и величины спроса, учитывая, что количество потребителей на путешествия в Испанию в связи с понижением цены увеличилось с 60 тыс. чел. до 80 тыс. чел. получим следующее значение коэффициента ценовой эластичности:

.

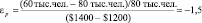Эластичность – 1,5 означает, что если бы цена понизилась на 10 %, то спрос туры в Испанию возрос бы на 15 %. Обычно для простоты знак «минус» опускают, используя абсолютную величину эластичности.

При эластичном спросе, когда эластичность по цене больше 1, общая выручка (P×Q) возрастает быстрее по сравнению с темпами снижения цены. Когда спрос эластичен, падение цены повлечет за собой одновременное повышение спроса и увеличение объема продаж, а, следовательно, будет результатом более высокой общей выручки. А если бы цена росла, то общая выручка падало бы, так как при эластичном спросе повышение цен сопровождается еще большим падением спроса и уменьшением объема продаж [11].

И напротив, при неэластичном спросе падение цен снижает общую выручку (общая выручка возрастает медленнее по сравнению с темпами снижения цены). Если же эластичность равна 1, то темпы изменения цен и общей выручки адекватны.

Среди большого разнообразия экономико-математических методов, используемых для решения задач управления туристской фирмой, особое место занимают методы и модели прогнозирования.

Для математических методов прогнозирования характерен подбор и обоснование математической модели исследуемого процесса, а также способов определения ее неизвестных параметров. Задача прогнозирования при этом сводится к решению уравнений, описывающих данную модель для заданного момента времени.

Среди математических методов прогнозирования в особую группу выделяются методы экстраполяции, которые отличаются простотой, наглядностью и легко реализуются на ПЭВМ. Методологическая предпосылка экстраполяции состоит в признании преимущественной связи между прошлым, настоящим и будущим. При этом развитие экономических явлений наиболее полно находит свое отражение во временных рядах, которые представляют собой упорядоченные во времени наборы изменений каких – либо характеристик изучаемого объекта, процесса [12].

В ходе решения задач прогнозирования пользуются ограниченным количеством информации об одномерном временном ряде конечной длины. При этом в экономике исследуются дискретные временные ряды, наблюдаемые в дискретные моменты времени.

Дискретный временной ряд можно рассматривать как последовательность значений y1, y2,… yn в моменты времени t, или сокращенно yt (t = 1,2, …, n).

Временной ряд может быть представлен в следующем виде:

yt = xt' + et', (4)

где xt' – детерминированная неслучайная компонента процесса, et' – стохастическая случайная компонента процесса. Детерминированная компонента (тренд) xt' характеризует существующую динамику процесса в целом, длительную тенденцию изменения изучаемого показателя. Стохастическая компонента et' отражает случайные колебания или шумы процесса (4). Задача прогнозирования, в частности, состоит в определении вида экстраполирующих функций xt' и et' на основе эмпирических оценок [13–16].

При прогнозировании, как правило, в точке прогноза оценивается математическое ожидание процесса (точечный прогноз) и величину интервала, в которой с заданной вероятностью попадает прогнозируемое значение процесса (интервальный прогноз). Результаты экстраполяции наиболее надежны при кратко – и среднесрочном прогнозировании. При этом предполагается, что совокупность факторов, определяющих тенденцию временного ряда в прошлом, в среднем сохранит свою силу и направление действия в течение прогнозируемого периода.

В настоящее время разработана большая группа экстраполяционных методов прогнозирования отдельных экономических показателей. В данной группе методов можно отнести:

1. Методы, основанные на построении многофакторных корреляционно – регрессионных моделей.

2. Методы авторегрессии, учитывающие взаимосвязь членов временного ряда.

Авторегрессионные модели чаще всего используются для прогнозирования тех экономических процессов, для которых внешний механизм их формирования четко не определен, и практически невозможно выделить стабильные во времени причинно – следственные связи.

Библиографическая ссылка