Научный журнал

Международный журнал экспериментального образования

ISSN 2618–7159

ИФ РИНЦ = 0,425

• Авторы
• Файлы
• Литература

Барышевский С.О. 1

---

1 Мелитопольский государственный педагогический университет имени Богдана Хмельницкого

Статья в формате PDF

857 KB

1. Раскин Л.Г., Серая О.В. Нечеткая математика. Основы теории. Приложения. – Х.: Парус, 2008. – 352 с.

2. Берштейн Л.С., Боженюк А.В. Нечеткие графы и гиперграфы. – М.: Научный мир, 2005. – 256 с.

3. Новак В., Перфильева И., Мочкорж И. / пер. с англ.: под ред. Аверкина А.Н. – М.: Физматлит, 2006. – 352 с.

4. Баришевський С.О. Основи теорії точкових нечітких множин // Праці: Таврійський державний агротехнологічний університет. – Мелітополь: ТДАТУ, 2012. – Вип. 4. – Т. 52. – С. 141–144.

5. Баришевський С.О. Точкові нечіткі множини та їх відображення // Праці: Таврійський державний агротехнологічний університет. – Мелітополь: ТДАТУ, 2012. – Вип. 4. – Т. 54. – С 3–8.

В последнее время рассмотрение основных вопросов теории нечетких множеств проводится в основном без широкого привлечения аппарата нечеткой логики [1]. Так же, как в основе теории четких множеств лежит четкая логика, в теории нечетких множеств по нашему мнению должна использоваться нечеткая логика как в узком (FL.n), так и в широком (FL.b) смысле [3].

В данной работе мы предлагаем рассмотрение основ теории нечетких множеств и понятия системы нечетких множеств с привлечением аппарата нечеткой логики.

Основные понятия теорий нечетких множеств и нечёткой логики будем полагать такими же как и в [1–5].

Рассмотрим основные операции над нечеткими множествами. Пусть и – нечеткие множества в Х, причём

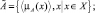
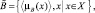
где величины μ_A(x) и μ_B(x) понимаются как нечеткие высказывательные переменные.

Введем понятие степени включения 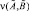нечеткого множества в нечеткое множество , которое находится по формуле

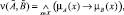
где «→» – операция нечеткой импликации, а 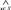– операция нечеткой конъюнкции, которая берется по всем x ∈ X. Естественно, что аналогичным образом можно определить и степень включения 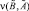нечеткого множества в множество [2; 4].

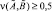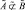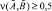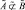Если , то будем полагать, что множество нечетко включается во множество , и обозначать . Если , то считаем, что множество нечетко не включается во множество , обозначается [2; 4].

Определим степень равности нечетких множеств и выражением

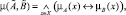
где «↔» – операция нечеткой эквивалентности. Если 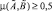, то будим полагать, что множества и нечетко равны, и обозначать 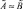. Если 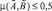, то считаем, что множества и нечетко не равны, и обозначаем 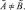В случае, когда 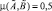, множества и одновременно нечетко равны и не равны. Эти множества называют взаимно индифферентными и обозначают 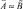[2; 4].

Есл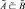и и 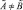, то будем говорить, что нечетко строго включается во множество .

Объединением множеств и назовем нечеткое множество определяемое как

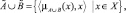
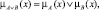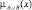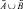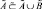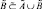где здесь ˅ – нечеткая дизъюнкция, а – нечеткое высказывание, определяющее степень принадлежности элемента x ∈ X множеству которое является таким, что и [2].

Пересечением множеств и называется нечеткое множество определяемое как

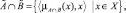
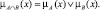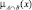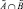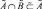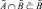где Здесь нечеткая конъюнкция, а – нечеткие высказывание, определяющее степень истинности принадлежности элемента x ∈ X множеству , которое является таким, что и [2].

Разностью множеств и называется нечеткое множество где

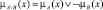
Здесь ¬ –операция нечеткого отрицания, а – нечеткое высказывание, определяется степень принадлежности элемента x ∈ X множеству .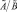

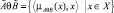Симметрическая разность и называется нечеткое множество , где 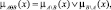которое является нечетким высказыванием, определяющим степень принадлежности элемента x ∈ X множеству .

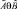Рассмотрим основные определения систем нечетких множеств. Системой нечетких множеств некоторого множества будем называть нечеткое множество, элементами которого являются нечеткие множества, 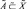. При этом Х – любое множество, содержащее все множества системы 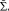однако, среди них всегда можно выбрать наибольшее, которое называется единицей системы 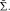Ясно что, единица нечетко совпадают с объединением всех нечетких подмножеств этой системы.

Кольцом нечетких подмножеств некоторого нечеткого множества называется система , замкнутая относительно операций нечеткого объединения, нечеткого пересечения, и нечеткой разницы, то есть из того что 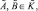следует, что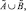 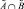, 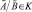. Очевидно, что нечеткая симметрическая разность также принадлежит кольцу.

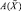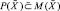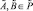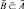Алгеброй нечетких множеств называется кольцо, содержащее единицу . σ – кольцом называется нечеткое кольцо, замкнутое относительно операции нечеткого счетного объединения; σ – алгеброй, называется σ – кольцо с . Полукольцом нечетких подмножеств некоторого множества называется система , замкнутая относительно операции нечеткого пересечения, содержащая и такое, что если , , то , .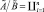

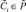В данной работе изложено элементы теории нечетких множеств и рассмотрены основные системы нечетких множеств с привлечением аппарата нечеткой логики как в узком так и в широком смысле. Полученные в работе результаты в дальнейшем могут быть использованы для построения теории меры абстрактных нечетких множеств.

Библиографическая ссылка