Постановка задачи
Для решения задачи о моделировании нестационарных волн в упругих деформируемых средах рассмотрим некоторое тело Г в прямоугольной декартовой системе координат XOY (рис. 1), которому в начальный момент времени 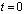 сообщается механическое воздействие. Предположим, что тело Г изготовлено из однородного изотропного материала, подчиняющегося упругому закону Гука при малых упругих деформациях.
сообщается механическое воздействие. Предположим, что тело Г изготовлено из однородного изотропного материала, подчиняющегося упругому закону Гука при малых упругих деформациях.
Точные уравнения двумерной (плоское напряженное состояние) динамической теории упругости имеют вид
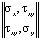 ×
× =
=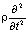
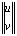 ,
, 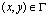 ,
,
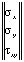 =
=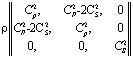 ×
×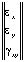 ,
,
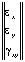 =
=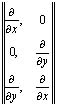 ×
×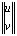 ,
, 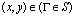 , (1)
, (1)
где 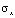 ,
, 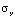 и
и 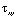 – компоненты тензора упругих напряжений;
– компоненты тензора упругих напряжений; 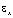 ,
, 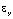 и
и 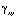 – компоненты тензора упругих деформаций; u и
– компоненты тензора упругих деформаций; u и 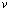 – составляющие вектора упругих перемещений вдоль осей OX и OY соответственно;
– составляющие вектора упругих перемещений вдоль осей OX и OY соответственно; 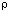 – плотность материала;
– плотность материала; 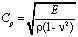 – скорость продольной упругой волны;
– скорость продольной упругой волны; 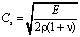 – скорость поперечной упругой волны;
– скорость поперечной упругой волны; 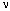 – коэффициент Пуассона; E – модуль упругости;
– коэффициент Пуассона; E – модуль упругости; 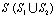 – граничный контур тела Г.
– граничный контур тела Г.
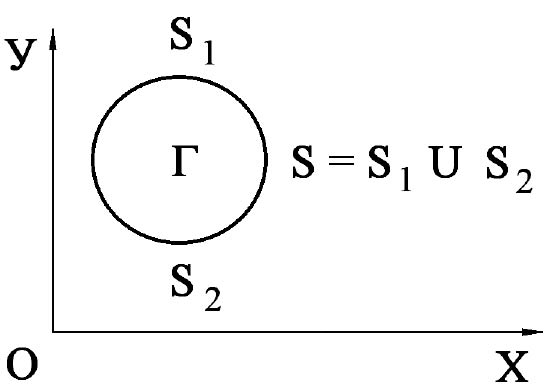
Рис. 1. Некоторое тело Г в прямоугольной декартовой системе координат XOY
Систему (1) в области, занимаемой телом Г, следует интегрировать при начальных и граничных условиях. Начальные условия в области Г зададим в виде
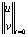 =
=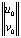 ,
, 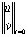 =
=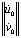 ,
, 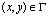 , (2)
, (2)
где 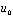 ,
, 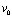 ,
, 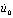 и
и 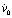 – заданные в области Г функции.
– заданные в области Г функции.
Граничные условия зададим в виде:
составляющих компонентов тензора упругих напряжений на границе 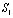
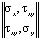 ×
×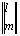 =
=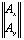 ,
, 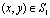 ; (3)
; (3)
составляющих компонентов вектора упругих перемещений на границе S2
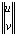 =
= ,
, 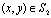 , (4)
, (4)
где l и m – направляющие косинусы; 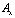 ,
, 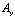 ,
, 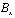 и
и 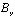 – заданные на границе S функции.
– заданные на границе S функции.
Разработка методики и алгоритма
Для решения двумерной плоской динамической задачи теории упругости с начальными и граничными условиями (1–4) – используем метод конечных элементов в перемещениях.
Постановки, численные методы, технология программных комплексов и анализ результатов решения нестационарных динамических задач для областей сложной формы рассмотрены в следующих работах [1–10].
Задача решается методом сквозного счета, без выделения разрывов. Основные соотношения метода конечных элементов получены с помощью принципа возможных перемещений.
Для решения линейных дифференциальных уравнений (1–4) используем метод конечных элементов в перемещениях.
Принимая во внимание определение матрицы жесткости, вектора инерции и вектора внешних сил для тела Г, записываем приближенное значение уравнения движения в теории упругости
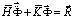 ,
, 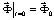 ,
,
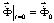 , (5)
, (5)
где 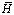 – матрица инерции;
– матрица инерции; 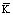 – матрица жесткости;
– матрица жесткости; 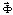 – вектор узловых упругих перемещений;
– вектор узловых упругих перемещений; 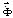 – вектор узловых упругих скоростей перемещений;
– вектор узловых упругих скоростей перемещений; 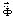 – вектор узловых упругих ускорений;
– вектор узловых упругих ускорений; 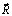 – вектор узловых упругих внешних сил.
– вектор узловых упругих внешних сил.
Соотношение (5) система линейных обыкновенных дифференциальных уравнений второго порядка в перемещениях с начальными условиями. Таким образом, с помощью метода конечных элементов в перемещениях, линейную задачу с начальными и граничными условиями (1–4) привели к линейной задаче Коши (5).
Матрица жесткости, вектор инерции и упругие напряжения в центре тяжести треугольного конечного элемента с тремя узловыми точками (рис. 2) представим в следующем виде
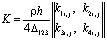 ; (6)
; (6)
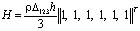 ; (7)
; (7)
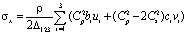 ,
,
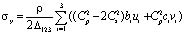 ,
,
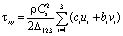 , (8)
, (8)
где 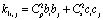 ;
;
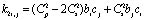 ;
;
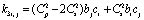 ;
;
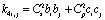 ;
;
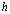 – толщина треугольного конечного элемента.
– толщина треугольного конечного элемента.
Матрица жесткости, вектор инерции и упругие напряжения в центре тяжести прямоугольного конечного элемента с четырьмя узловыми точками (рис. 3) представим в следующем виде
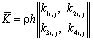 ; (9)
; (9)
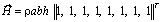 ; (10)
; (10)
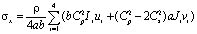 ,
,
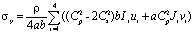 ,
,
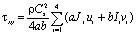 , (11)
, (11)
где 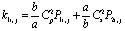 ;
;
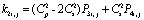 ;
;
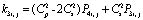 ;
;
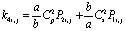 ;
;
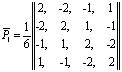 ;
;
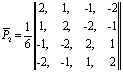 ;
;
 ;
;
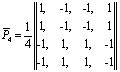 ;
;
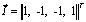 ;
; 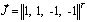 ;
;
h – толщина прямоугольного конечного элемента.
Определим упругое контурное напряжение на границе области, свободной от нагрузок. С помощью вырождения прямоугольного конечного элемента с четырьмя узловыми точками получим контурный конечный элемент с двумя узловыми точками (рис. 4).
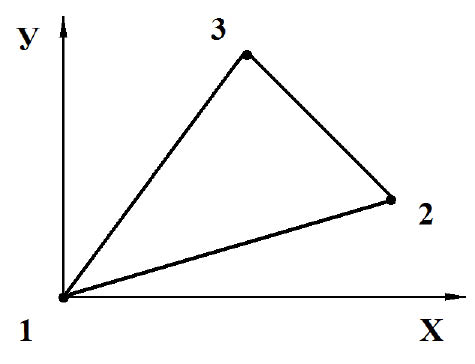
Рис. 2. Треугольный конечный элемент с тремя узловыми точками
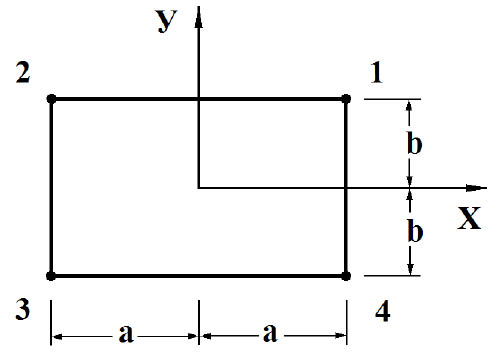
Рис. 3. Прямоугольный конечный элемент с четырьмя узловыми точками
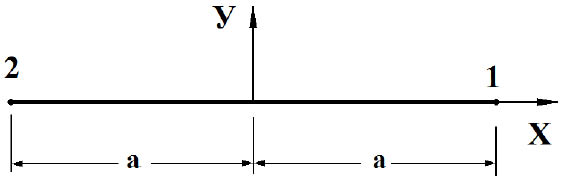
Рис. 4. Контурный конечный элемент с двумя узловыми точками
При повороте оси x на угол 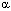 против часовой стрелки, получим упругое контурное напряжение
против часовой стрелки, получим упругое контурное напряжение ![]() в центре тяжести контурного конечного элемента с двумя узловыми точками
в центре тяжести контурного конечного элемента с двумя узловыми точками
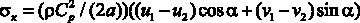 . (12)
. (12)
Рассмотрим интегрирование системы линейных обыкновенных дифференциальных уравнений второго порядка в перемещениях с начальными условиями.
Для интегрирования уравнения (5) конечноэлементным вариантом метода Галеркина приведем его к следующе
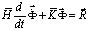 ,
, 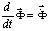 . (13)
. (13)
Интегрируя по временной координате соотношение (13) с помощью конечноэлементного варианта метода Галеркина, получим двумерную явную двухслойную конечноэлементную линейную схему в перемещениях для внутренних и граничных узловых точек
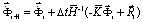 ,
, 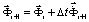 , (14)
, (14)
где 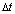 – шаг по временной координате.
– шаг по временной координате.
Основные соотношения метода конечных элементов в перемещениях получены с помощью принципа возможных перемещений и конечноэлементного варианта метода Галеркина.
Рассмотрим устойчивость двумерной явной двухслойной конечноэлементной линейной схемы в перемещениях для внутренних и граничных узловых точек на квазирегулярных сетках.
Система уравнений (14) для внутренних и граничных узловых точек, полученная в результате интегрирования уравнения движения теории упругости (5), должна давать решение, сходящееся к решению исходной системы (1–4).
Общая теория численных уравнений математической физики требует для этого наложение определенных условий на отношение шагов по временной координате и по пространственным координатам, а именно
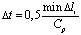
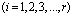 , (15)
, (15)
где 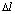 – длина стороны конечного элемента; r – общее число конечных элементов в исследуемой области.
– длина стороны конечного элемента; r – общее число конечных элементов в исследуемой области.
Для исследуемой области, состоящей из материалов с разными физическими свойствами, выбирается минимальный шаг по временной координате (15).
В работах [1, 3–6, 9] приведена информация об оценке математической и физической достоверности разработанного метода, алгоритма и комплекса программ.
На основе метода конечных элементов в перемещениях разработаны алгоритм и комплекс программ для решения линейных плоских двумерных задач, которые позволяют решать задачи при нестационарных волновых воздействиях на сложные системы. При разработке комплекса программ использовался алгоритмический язык Фортран-90. Исследуемая область разбивается по пространственным переменным на треугольные конечные элементы с тремя узловыми точками с линейной аппроксимацией упругих перемещений и на прямоугольные конечные элементы с четырьмя узловыми точками с билинейной аппроксимацией упругих перемещений. По временной переменной исследуемая область разбивается на линейные конечные элементы с двумя узловыми точками с линейной аппроксимацией упругих перемещений.
Библиографическая ссылка
Мусаев В.К. ЧИСЛЕННОЕ МОДЕЛИРОВАНИЕ НЕСТАЦИОНАРНЫХ ВОЛН В УПРУГИХ ДЕФОРМИРУЕМЫХ ТЕЛАХ // Международный журнал экспериментального образования. 2015. № 12-3. С. 342-346;URL: https://expeducation.ru/ru/article/view?id=9123 (дата обращения: 12.03.2026).

