Научный журнал

Международный журнал экспериментального образования

ISSN 2618–7159

ИФ РИНЦ = 0,425

• Авторы
• Файлы
• Литература

Матвеева А.Е. 1 Макарова Н.В. 1 Миронова Ю.Н. 1

---

1 Елабужский институт Казанского (Приволжскиого) федерального университета

Статья в формате PDF

0 KB

1. Математический анализ: Интегральное исчисление: Учеб. пособие для студентов-заочников 2 курса физ.-мат. фак. пед. ин-тов / Н.Я. Виленкин, А.Г. Мордкович, Е.С. Куницкая; Моск. гос. заоч. пед. ин-т. – 2-е изд., перераб. – М.: Просвещение, 1988. – 14 с.

2. Сборник задач по курсу математического анализа / Г.Н. Берман. – М., 1969. – 125 с.

Один из методов вычисления интегралов, называемый интегрированием по частям, основан на правиле дифференцирования произведения двух функций. Рассмотрим функции

,

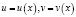дифференцируемые на некотором промежутке X. Согласно свойствам дифференциалов, имеет место следующее равенство:

.

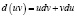Взяв неопределенный интеграл от обеих частей этого равенства, получим:

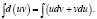
Так как:

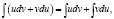
то получаем:

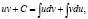
откуда

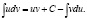
Мы получили формулу интегрирования по частям:

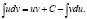(1)

Так как 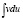существует по условию, то 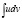тоже существует. Метод используется следующим образом. В 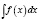выделяем u и dv, затем находим du, а из dv интегрированием находим 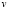и используем формулу интегрирования по частям. u и dv нужно выбрать так, чтобы:

Из dv легко находилась v; 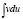вычислялся легче, чем .

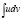Замечание. Иногда интегрирование по частям приходятся применять несколько раз.

Пример 1

Вычислить интеграл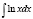

Решение: Положим

.

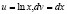Тогда

.

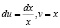Используя формулу (1), получим:

.

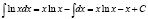Ответ: .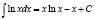

Пример 2

Вычислить интеграл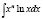

Решение: Положим

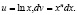
Тогда

.

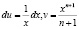Используя формулу (1), получим :

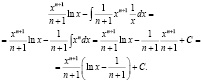
Ответ: .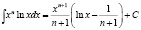

Пример 3

Вычислить интеграл .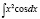

Решение: Положим

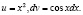
Тогда .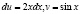

Используя формулу (1), получим :

.

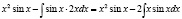Положим

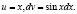
Тогда

.

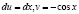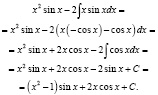
Ответ: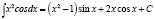

Пример 4

Вычислить интеграл: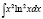

Решение: Положим

.

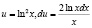Тогда

.

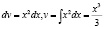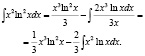
Положим

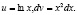
Тогда

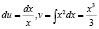
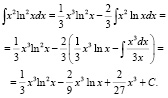
Ответ:

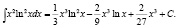
Библиографическая ссылка